- Why Subnet?
- Binary
- IPs, Masks, and Navigation
- Subnet by Hosts
- Subnet by Networks
- Subnetting in the Real World - VLSM
- Debugging - Reverse Engineering Subnets
Part 1 - Why Subnet?
Introduction
Welcome to my seven-part course on Subnetting.
Subnets are important. They're the equivalent of reproduction for networks, so if you're an aspiring network engineer you can consider this your "Come here, Bobby, we need to have a little talk about..." speech. We're not going to get kinky here, but we'll certainly cover the basics. Enough for you not to burst into tears and run to mummy when you see a network showing off its bits. I'll stop with the metapor. The point is subnets are important for network engineers.
If you know how to calculate a subnet for a given number of hosts on a given class of network, feel free to stop reading now, or to skip to the last two entries on reverse-engineering and VLSM. If you've never heard the word 'binary' before, you'll want to pay close attention to section 2 on binary arithmetic or you might end up getting lost quickly. Over this course we'll cover what subnets are and why we have them; the different classes of local (private) networks; how to calculate a subnet mask for a given number of hosts/network; and how to calculate a subnet mask for a given number of networks. Sounds like a lot? Well just think of all the new stuff you'll know by the time we've finished.
As a bonus for those of you who are still reading by the end, and have got the hang of subnetting by that point, we'll also take a look at VLSM - Variable Length Subnet Masks, how to address a network efficiently with them, and at reverse engineering a subnet mask, or how to work out which subnet you're on. Let's begin.
Glossary (these will be provided for all parts of the course, but things already covered will be left out of following glossaries):
Network - An infrastructure for communication between hosts
Subnet - A sub-network. Identical to a network except that it cannot be divided into further subnets
WAN - Wide Area Network, usually used to referr to the internet, although it can designate a private long-distance connection between offices
LAN - Local Area Network, a network covering a limited physical space, usually private to the place running it
Router - A networking device used to mark the boundaries of, and communicate between, networks
Switch - A networking device used to extend the physical coverage of a network
Host - A network device (eg. Computer, Router, Switch, etc.)
Network Traffic - Data passed over a network connection
Why Subnet?
The three key points to know about why we subnet are organisation, optimisation, and security. When we're dealing with subnetting public (WAN) networks as opposed to private (LAN) networks, they can also save us a hell of a lot of money. Or, more accurately, they save our clients a ton of money so we can charge a hefty fee to set them up.
Organisation
Subnets help us organise our network in the same way we might use different rooms in a house. Suppose we think of a network as the building itself. Without subnets it has no internal walls. It's just a box. So our toilet is indistinct from our kitchen, our bedroom might be next to our shower-room, and our washing machines might be nearby our study. Clearly this raises problems for us because if we live like this for more than a month or two we end up eating crap, sleeping on a damp matress, and unable to concentrate on anything without the continual burrrrrrrrrrr and hissssssss of the washing machine drowning out our thoughts and concentration, and reducing us to twitchy psychotics with bloodshot eyes. Actually some of us might live like that anyway, but let's imagine there's a better way.
Subnets would be that way. By putting internal walls in our house we can separate areas designated for one task from another. Our kitchen is now our kitchen, our toilet our toilet, our shower our shower, etc. Excellent. Similarly, a company might want to separate sales from tech support, marketing from engineering (to reduce electrocution casualties in the marketing people), and everyone from the budget system. They might want to allow only sales people to access the sales printers and sales servers. So we divide them into different networks.
Optimisation
Now we come to broadcasts. A broadcast is a type of network traffic, and it is unique in that it is sent to everyone on the network. Every device on the network recieves a broadcast up until it reaches a router. Routers stop broadcasts. That's their primary function. Yes, they can switch traffic between networks, manage port forwarding, etc., but their primary requirement by design is to stop broadcasts. Think of them as insulated walls in our house.
We put up walls so our bed no longer gets soaked by the shower. But the sound of the washing machine might still annoy us while we're reading. Not anymore. These walls are insulated, so we aren't concerned by what the washing machine is doing. It can shake itself to pieces trying to get the stench of humiliation out of that pair of underpants you were wearing when you went 0-8 in Counter-Strike against some twelve year-old using only the knife, and it still won't disturb you while you're indulging your fetish for Victorian Science Journals.
The noise of the washing machine represents our broadcasts. Computers send broadcasts all the time. Many routers and switches do likewise (especially older ones). So networks are noisy. Subnetting helps by reducing the number of hosts on a network, and thus reducing the amount of noise on the network. Fewer hosts sending out broadcasts equals fewer broadcasts equals fewer unnecessary packets recieved by each host. You can support about 500 hosts on a network before you start to get slowdown (regardless of the wire speed), but it is good practice to subnet for much lower numbers.
Sidenote - Types of traffic, uni-, multi-, and broadcast
Network traffic can be divided into three supertypes: unicast, multicast, and broadcast.
Unicast traffic is sent from one host to another.
Multicast traffic is sent from one host to a group of other hosts.
Broadcast traffic is sent from one host to every other host on the network.
Technically there is a fourth type, anycast, which is a multicast system whereby the traffic is sent to the nearest hosts rather than hosts which have asked to recieve the multicast traffic.
Security
Most homes don't require internal security, so our analogy is in danger of falling apart here, but let's assume for the moment you're a right-wing, Bush-voting, cerebrally-challenged-enough-to-be-proud-of-it gun nut. You have an impressive array of firearms such that you could wipe out a couple of hundred species of endangered mammals without stopping to reload. Because you rightly understand that the place for your weaponary (aside from the rifle in the umbrella stand, the uzi in the play room, the glock under the pillow, and the shotgun in the woodshed) is securely locked away from unauthorised hands, you have a gun room. This room has a lock, so people who are in your house are unable to access your gun room without authentication.
Subnetting helps us once again here. Each door in your house (because we're smart enough to know that walls are pretty useless without doors) can be considered a router. Routers handle moving traffic between networks (rooms). We can tell routers to only allow access from certain networks, or from no networks at all. So now we have locks on our gun-room door, and security in our subnets.
The computer-savvy engineering boffin can no longer access the payroll server and add a couple of zeroes to his salary. At least not as easily as he could before (where there's a will, there's a way, and where there's personal financial benefit there's usually a will).
Summary
That's why we subnet. For organisation, optimisation (efficiency), and security. Join me next time for a look at binary arithmetic and hopefully we'll get the hang of the basics necessary for working with subnets.
Part 2 - Binary
Introduction
You've probably heard about binary before. You almost certainly know that computers work exclusively in binary. You may even know how to do mathematics in binary and bitwise operations. If you know that last one then you can jump ahead. This section is designed to give the binary novice an explaination of binary and how to work with it. For those of you who have tried to learn binary before, I hope you will give me a chance to explain it here. I will attempt to explain the key concepts in a variety of different ways, and hopefully one will stick.
First we will be looking at counting systems with different bases. We're all familiar with decimal (base 10), but we'll understand exactly what decimal is, why it works, and how that relates to different bases. After that we will have a look at some of the specifics of binary itself, and consider how computers use binary (which is slightly different to how we would use it). Finally we'll look at the parts of binary arithmetic we will need to know for working with subnets. The arithmetic isn't complex, in fact it barely counts as arithmetic. All we really need to know is how to convert between binary and decimal, and we will be covering that here.
We will have some exercises. You do not have to do these but you will probably gain more from this section if you do.
Glossary:
Decimal - the base 10 number system
Binary - the base 2 number system
Base - a base x number system has x digits available (0 through x), and each column is x to the power of the number of previous columns
Note:
Previously and after this I will use code tags, but for this part is is important that you see how numbers relate. I will be using colour to distinguish and associate them, so I will be using quote tags and inserted images instead.
What is Decimal?
We are all competent, to some degree or another, with the decimal, or Base 10 number system. Some of us can multiply large numbers in our heads, others can do little more than count and recite basic times tables. The good news is that we don't need more than the ability to add or subtract decimal numbers (and not very big ones).
What is the Base 10 number system? How could there be other ones? Well, let's have a look at what we mean by Base 10:
Base 10 means that we have ten digits and column values which are powers of ten. Let's have a close look at those:
Quote
Decimal Digits:
0 1 2 3 4 5 6 7 8 9
Decimal Column Values:
Units (1s) = 10^0 (ten to the power of zero)
Tens (10s) = 10^1
Hundreds (100s) = 10^2 (10x10 = 100)
Thousands (1000s) = 10^3 (10x10x10 = 1000)
etc.
Alright, hold up. Question time. Why did you stop counting digits at 9? Because any number higher than 9 is not a decimal digit. It is made up of decimal digits, but it must contain more than one. 10 is the digits 1 and 0. Eleven is 1 and 1.
Now you're just making me mad. 1 and 1 is two. You got me. Eleven isn't actually 1 and 1. It's made up of the digits 1 and 1, but the true value of a digit is equal to the digit value times the column value. I'll show you:
Quote
Notice how we never have to do any carrying over? Of course we don't, because if we did we couldn't represent the right value. We couldn't have 10 in the 100s column, because 10x100 = 1000, so we'd have 1 in the 1000s column and 0 in the 100s column instead. That's the key behind decimal. Decimal means base 10, and that means it has ten different digits and each column is 10 to the power of the number of columns that came before.
Okay, but what is all this about powers of stuff? Alright, I just said that each column value in decimal is 10 to the power of the number of preceeding columns. What do we mean by 10 to the power of something? We mean that we do 10 multiplied by 10 that many times.
Quote
The ^ symbol is used in many programming languages to mean 'to the power of', so we'll use that here.
10^1 = 10
10^2 = 10x10 = 100
10^3 = 10x10x10 = 10x100 = 1000
10^4 = 10x10x10x10 = 10x1000 = 10000
10^5 = 10x10x10x10x10 = 10x10000 = 100000
In decimal it's easy because the power tells us how many 0s we have after the 1. The others don't work so well, but we'll get the hang of them. We also need to know two special cases here: any number to the power of zero is one; and any number to the power of one is itself.
Binary
Now to binary. Binary is the base 2 number system. Let's work through what we know from examining decimal and apply it to binary. First, we know that if the number of digits available to decimal is 10, the number available to binary must be 2. Second, we know that because the column values in decimal are powers of 10, so the column values of binary must be powers of 2.
Let's have a look at converting a number from decimal to binary. First we'll identify the columns:
Quote
2^0 = 1
2^1 = 2
2^3 = 4
2^4 = 8
2^5 = 16
2^6 = 32
2^7 = 64
2^8 = 128
So the columns for a binary value are:
128s, 64s, 32s, 16s, 8s, 4s, 2s, and 1s.
Of course the columns can increase indefinitely, just as the number of columns in a decimal system can, but why we're only dealing with eight columns will become clear in the next section.
Let's have a look at the largest number we could write with eight columns.
Quote
So there we have it, the highest decimal number we can get with eight columns is nine-hundred and ninety-nine million, nine-hundred and ninety-nine thousand, nine-hundred and ninety-nine. What about doing that with binary?
Quote
So 255 is the largest number we can write in binary with eight digits.
I know this may have been quite complicated thus far, but let's press on and see if we get the hang of converting binary numbers to decimal and vice versa.
Converting between Binary and Decimal
Now we know what binary and decimal are we can convert between them. We've actually converted a binary number to decimal already. We worked out that the highest 8-digit binary number, 11111111, is 255 in decimal. Let's take a close look at converting a binary number to decimal. I really want the columns to be obvious here, so I'll write them vertically.
Quote
So we get the decimal value of a binary number by adding up the values of the columns with ones. Here are some exercises for you to practice with. So we can tell binary values from decimal ones, we'll write all binary numbers as 8-digit numbers and pad the front with 0s where necessary. So 5, which is 101 (4+1) in binary, we would write as 00000101. That way we won't get confused between 101 as a binary 5, and as a decimal 101. There is a very good reason for this which will become clear when we look at how computers use binary.
Exercise - Converting Binary to Decimal
Here are some binary numbers to convert to decimal:
- 00000011
- 10101010
- 11000000
- 11100001
- 00010001
- 00100100
- 11110000
- 11111100
- 00000000
Once you have done those, check them against my answers here. My working is shown, but you may have been able to do it without.
Answers:
- 00000011 = 2+1 = 3
- 10101010 = 128+32+8+2 = 170
- 11000000 = 128+64 = 192
- 11100001 = 128+64+32+1 = 225
- 00010001 = 16+1 = 17
- 00100100 = 32+4 = 36
- 11110000 = 128+64+32+16 = 240
- 11111100 = 128+64+32+16+8+4 = 252
- 00000000 = 0
You probably found yourself becoming much quicker, and you may have found clever shortcuts (11111110 is the maximum 255 - the missing 1, so 254, for example). If you found it difficult, I suggest you come up with a few binary numbers of your own and practice a bit. It should not take long before you master the process, and eventually you'll be able to read binary as easily as decimal. I'm not there yet, though, so don't rush it.
Converting Decimal to Binary:
This is a very similar process, except instead of adding up the columns instead we take the columns away from our starting decimal number once we have used them. Because we can only put 1 in any column, we can only use each column once. Let's have a look:
Quote
And that's it. All you have to remember is:
- Take the biggest column value that is less than or equal to the number you have.
- Put a 1 in that column.
- Take that column value away from the number you had, and that's your new number.
- Repeat until you have 0 left.
- Put 0s in any columns which do not have 1s in.
Exercise - Converting Decimal to Binary
Here are some numbers to convert to binary. Remember to write them all as 8 digits, and off you go:
Answers:
- 17 = 00010001
- 182 = 10110110
- 64 = 01000000
- 111 = 01101111
- 168 = 10101000
- 202 = 11001010
- 37 = 00100101
- 89 = 01011001
You can make up more examples for yourself. Remember you can check them by converting back from binary to decimal.
That's all there is to converting, and you'll get quicker the more you do it.
Binary for Computers
I told you we would be padding binary numbers to 8 digits, and I told you there was a very good computery reason why. Well here's the reason. You've heard of bytes. Or at least megabytes, gigabytes, and kilobytes. Well a byte is a measurement of size for information. A byte is equal to 8 bits, and bits are 1s or 0s.
Computers work in bytes, and a byte is 8 bits. A bit is a 1 or a 0, so computers work in blocks of 8-digit binary numbers (eight slots which are either a 1 or a 0). So when we pad 64 to look like 01000000 in binary, we're showing it the way a computer would. That is why we work with 8 digits, and also why none of the examples I gave you were larger than 255 (because 255 is the largest value we can show with just 8 binary digits).
Of course, computers can handle numbers larger than 255, and they can do lots of other awesome things (TF2, anyone?), but fundamentally they're always dealing with bits in bytes. We'll see them dealing with that a lot when we get on to the next section in the course.
Summary
Alright, we've covered a lot, so go and relax for a bit. We've covered what decimal actually is, and we've worked with binary. We've seen how we can convert binary numbers to decimal and back again. We've even seen how computers handle binary and learned why we tend to express binary numbers as 8-digit numbers, even though we may not need all 8 digits to show a number.
Before you go back to your decimal world, I'll leave you with this final though: if you want to count higher than 10 on your fingers, try counting in binary. A finger down for a 0, and up for a 1. You can actually count to 1023 on your fingers and thumbs using binary. Cooler than the mere 10 for decimal, huh?
Join me next time for a look at IP addresses, Subnet Masks, and a brief overview of how computers navigate networks.
Part 3 - IP, Masks, and Navigation
Introduction
We've covered the reasons for subnetting, and we've learned how to convert between binary and decimal. This is the last topic before we hit the actual subnetting examples. Here we will discuss the IP (internet protocol) addressing system, subnet masks, and how computers navigate over networks. This will be the section to come back to if you get lost when dealing with subnets later on and want to refresh your memory as to what you're actually doing.
Glossary:
IP Address - an Internet Protocol address. We will be using IPv4 which is a four-byte address
Subnet Mask - a bitmask used to exclude bits in an IP address which pertain to the network
Wildcard Mask - a bitmask used to exclude bits in an IP address which pertain to the host. The opposite of a subnet mask
Host Mask - a wildcard mask
Hop - an crossover point between networks on the route between a source network and a destination network
IP Addresses
This is the last time we will be dealing with IP addresses as seperate from a subnet mask, so let's make the most of it. An IPv4 (IP version 4) address is a four-byte logical address that identifies a device. We will use IPv4 because it is simpler than IPv6, and at the moment more widely used. The device in question could be any network-capable device - a computer, printer, router, switch, etc.
So, let's look at an IP address. Let's start with the IP address belonging to the computer upon which I am writing this article. If you want to find out what your IP address is, you can use the ipconfig (ifconfig on Linux) command to find out. My IP address is 192.168.0.6. Now let's examine how the address is constructed.
192 . 168 . 0 . 6
IPv4 is a 4-byte address:
Byte1: 192
Byte2: 168
Byte3: 0
Byte4: 6
Each byte is 8 bits (1s or 0s), and, as we learnt in the section on binary, each byte can range from 0 to 255.
Here are our bits as binary numbers:
Byte1: 11000000
Byte2: 10101000
Byte3: 00000000
Byte4: 00000110
Alright, so we look at addresses in decimal for the sake of ease, but computers see them in binary. Here's the same process in a more visually appealing manner:

Now we know that an IP address is really a string of bits grouped into bytes. Realising IP addresses are a set of 4 bytes will be very important when we come to subnet masks and how they work. So, without further ado, let's look at subnet masks.
Subnet Masks
IP Classes
IP addresses can come in all shapes and sizes, from 0.0.0.0 to 255.255.255.255 (or very nearly, anyway). The body responsible for selling and giving away IP addresses, the Internet Assigned Numbers Authority (INAN, managed by the Internet Coperation for Assigned Names and Numbers, ICANN), has allocated certain blocks to be used only by certain people, or only for certain things. You might know about 127.0.0.1 (as in "there's no place like 127.0.0.1"), which is the loopback address, and essentially points any network device back to itself. 127.0.0.1 is from the 127 block, and that entire block is reserved for loopback addresses. Other blocks are reserved for the military, for managing the internet, for multicast notations, and various other things. The blocks which aren't reserved are sold to ISPs, who split them into smaller blocks, and eventually get to you usually in the form of a single IP address which you use to search the internet and work out how much Wikipedia you can put into your essays without getting caught.
The blocks come in different sizes. We'll have a look at the main ones you need to know:
Blocks starting with 1 through 126 are known as CLASS A addresses.
Blocks starting with 128 through 191 are known as CLASS B addresses.
Blocks starting with 192 through 223 are known as CLASS C addresses.
And some special cases:
Blocks starting with 127 are loopback addresses.
Blocks starting with 169.254 are autoconfig addresses.
Sidenote - Address Classes in Binary
If you're really up on your binary you may have noticed that all class A addresses would start with a 0 when written in binary. All class B would start 10, and all class C would start 11. Neat, huh?
So what do the classes mean? Classes define how big a block is. Essentially the class tells you how much of the address is taken up in sorting out which block it belongs to. Class A addresses have one byte identifying the block. Class B have two. Class C have three.
Each class has a private address block which anyone can use on their local network. Usually we see class C addresses, but the others are equally valid. Let's look at the blocks for Class A and Class B:
Private Address Blocks:
Class A: 10.
Class B: 172.16.
Notice that class B has two bytes specified. Class A has only one. Class C will have three bytes specified, but INAN generously allowed us 256 different blocks from Class C to use on our networks. How kind. Let's have a look at them:
Private Address Blocks:
Class C:
192.168.0.
192.168.1.
192.168.2.
...
192.168.254.
192.168.255.
Each one has three bytes taken up telling us what block it is from. And here we meet subnet masks.
My First Subnet Mask
The job of a subnet mask it to tell a device which bits denote the network. To understand this process we need to understand the bitwise AND operator. There are four bitwise operators. The only one we need here is AND. Quite simply, AND compares two bits, and sets the result bit to 1 if both bits are 1. If either or both of them is 0, the result is 0. This can be expressed as a truth table thus:
0 AND 0 gives 0
1 AND 0 gives 0
0 AND 1 gives 0
1 AND 1 gives 1
In effect, this operation allows the subnet mask to determine which bits the device cares about when looking for the network. Any bit with a 0 in the subnet mask will automatically be a 0 in the result, so the device doesn't care what the IP address has there. The device only cares about the bits which have a 1 in the subnet mask. Thus we can use the bitwise AND (the "I care about this bit" process) to work out which network a device is on.
Let's have a look at it in action for the fist byte of the address and the first byte of the subnet mask.
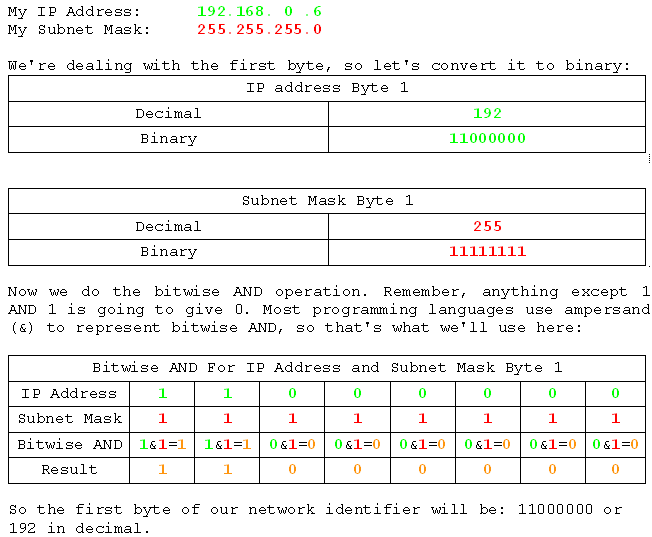
Now we'll do the AND operation on all four bits, but in a much more condensed way. If you get lost, try writing out the table above and going through the process for each bit in each byte.
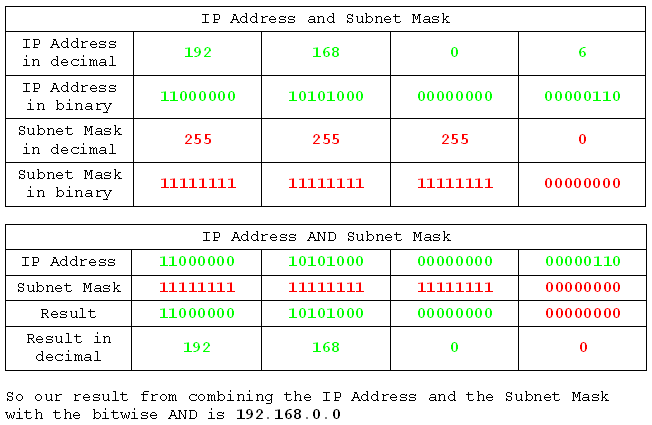
There's something special about 192.168.0.0. It is in fact the network ID. We would refer to this network as the 192.168.0 network, but what we would actually mean was the 192.168.0.0 network. If we were talking to computers about it we would have to call it the 192.168.0.0 network or they would not know what we were on about because we'd be giving them a three byte address, and every computer know that IPv4 addresses are four byte addresses. So there we have it. A bitwise AND operation on the IP address and the Subnet Mask yields the network ID.
Slash Notation and Default Subnet Masks
Each of the different classes has a default subnet mask. Remember that Class A was a block containing everything beginning with a Class A first byte? Well that means the Class A blocks have a default subnet mask which only cares about the first byte:
Class A: 1-126
Default Subnet Mask: 255.0.0.0
So your class A address has one byte saying which network it's on, and all the other bits in all the other bytes are zero. So the device doesn't care what it has in the IP address because it knows that it doesn't represent the network.
Class B has two bytes which specify the network:
Class B: 128-191
Default Subnet Mask: 255.255.0.0
Once again, all the bits in all the bytes beyond the second are zero, so the device doesn't care what they are in the IP address, because they won't represent the network.
For class C we see the same thing, only this time for the first three bytes:
Class C: 192-223
Default Subnet Mask: 255.255.255.0
And, as we saw in our example using my class C address 192.168.0.6, the device doesn't care about the last byte. So we got 192.168.0.0. It does care about bits which have a 1 in the subnet mask, though, so 192.168.1.6 is a different network to 192.168.0.6. And likewise 172.16.0.6 is a different network to 172.17.0.6. The class A network only cares about the first byte, though, so 10.1.0.6 is on the same network as 10.0.0.6.
Slash Notation
Slash notation is one of those things which looks far more complicated than it actually is. All slash, or CIDR notation, simply tells us how many 1s are in subnet mask when we write it in binary. so 255.0.0.0, which has 8 1s in the first byte, and none after that, is written as /8. The slash notation is usually appended to a network ID. To give you an idea, I'll show you the private address ranges we discussed earlier with slash notation:
Private Address Ranges:
Class A: 10.0.0.0, Subnet Mask 255.0.0.0
Class B: 172.16.0.0, Subnet Mask 255.255.0.0
Class C: 192.168.0-255.0, Subnet Mask 255.255.255.0
Slash Notation:
Class A: 10.0.0.0 /8
Class B: 172.16.0.0 /16
Class C: 192.168.0-255.0 /24
Now, having subnet masks like 255.255.255.0 (/24) is useful, because it lets us determine quite easily which network we're on. 255 means we care about the byte, 0 means we don't. But what if we want more networks? What if we want to break a Class B network into lots of Class C networks? Or what if we want to use things other than 255? Or slash notation like /30? Well that's where subnetting comes in, and we'll get right to that after we've had a very quick look at how computers navigate.
Network Navigation
Network devices only know about devices on their network. You can try it if you like. Set your IP address to something on a different network to your router and watch it fail to communicate with anything. So if you're currently on 192.168.0.0 / 255.255.255.0, try setting your IP and Subnet Mask to an address starting with 10 and a subnet mask of 255.0.0.0. Your connections will die horribly and instantly.
Once you've restored your IP address, or just gone back to using DHCP (automatic) addressing, we can continue.
So, devices only know about devices on their network. Which is bad news for inter-network communication (think inter-net communication). So we're screwed? Not really. We have routers. And a router connects to multiple networks at the same time, and can route traffic between them. Routers mark the boundaries between networks, and act as the crossing points between them. Every device which is allowed off its own network has a router which is very special to it. This router is known by a special title.
The default gateway. The role of a default gateway is to handle traffic sent to a destination which is on some foreign network. Any time a device needs to get off its network, it sends the traffic to its default gateway. Incidentally, routers have a default route which is essentially a default gateway for routers, and it's where they send traffic they don't know how to handle, i.e. traffic to networks they aren't directly plugged into.
And that, in a nutshell, is how a device can communicate with devices on different networks. By using its default gateway.
Summary
And now, as the computer and its default gateway walk off into the sunset, hand in hand, let's review what we learned. We learned that IP addresses are assigned in blocks of different sizes, and the sizes are related to the Class. We learned that each class has a default subnet mask, and how to write those masks in decimal, binary, and slash notation. We looked at how a subnet mask is used to identify the network, and we looked at how a device communicates over network boundaries.
Next time we will see how we break our big network chunks up into smaller networks, and get into the practical process of subnetting. Bring a pencil and paper.
Part 4 - Subnet by Hosts
Introduction
Now we should be ready to do our first subnet. So far we've seen how IP addresses are made, how a device works out the network from the IP address using the subnet mask, and we've even seen a couple of examples of the most basic /8, /16, and /24 subnet masks (255.0.0.0, 255.255.0.0, and 255.255.255.0) which are the defaults for classes A, B, and C. What we're about to do is answer some of the question we may have had about the default subnet masks, and then go right into an example of subnetting based on how many hosts are required in a network.
Glossary:
Network Range: a range of IP addresses belonging to a network. The first address is the network ID, the last is the broadcast. The others are addresses which can be assigned to devices.
Note:
Any information not directly related to subnetting, such as the descriptions of problems and examples, is liable to be wildly inaccurate.
Non-default Subnet Masks
With the /8, /16, and /24 subnet masks each byte was assigned to either the network or the host. So in a class A (/ network, the first byte (first 8 bits) designates the network, and the rest identifies the host on that network. We could use a non-default subnet mask, though, like /26. Let's see what that would look like in binary:
network, the first byte (first 8 bits) designates the network, and the rest identifies the host on that network. We could use a non-default subnet mask, though, like /26. Let's see what that would look like in binary:
/26 Subnet Mask
11111111.11111111.11111111.11000000
As a bonus we can convert it to decimal, because we learned how to do that.
/26 Subnet Mask in decimal:
/26 Subnet Mask
255.255.255.192
So there are our 26 1s in the mask. The new thing is that this time the last byte is split. Part of it designates the network, and the rest identifies the host. That might seem a little weird, but what if I were to tell you that you could do the same thing with decimal? We do, actually. Often used as part of an order number, for example, consider this number:
20090902
At first glance it looks like 20 million, 90 thousand, and 2. But we could also look at it like this:
20090902
Hmm. So it might be 2009/09/02 which would be a date. With any date we would always have an eight-digit number. It doesn't matter that it's all expressed as a single number because we know where to break it up. We have the digits for the year, the digits for the month, and the digits for the day. IP's subnet mask works in exactly the same way. We have digits for the network, digits for the host, and the subnet mask tells us which is which.
We are about to split a network into smaller networks by increasing the number of network bits. So let's get on with it.
Subnet By Hosts - Walkthrough
Let's roll.
I want to split my home network up into subnets of 40 hosts each (I live in a mansion which is practically made of computers). I don't want to change from my current 192.168.0 network, so we'll use that.
First I analyse the problem:
Subnet by Hosts
Network: 192.168.0.0
Subnet Mask: 255.255.255.0
Requirement: 40 hosts
So there's the info. I've got my class C network with its default /24 subnet mask and I need to split it into 40-host networks. First rule: always add 1 to the host requirement. We do this because two of the addresses on any network are already taken. Those are the network id (the first address), and the broadcast (the last address). Given that we count from 1, and networks start from 0, the network id is already covered, so we only have to reserve an extra one for the broadcast address. So I adjust my analysis:
Subnet by Hosts
Network: 192.168.0.0 /24
Requirement: 40+1 hosts
Notice I've added slash notation to the network field and removed the subnet mask. I've done that for speed and convenience, and you'll see why.
Now I need to find out how many bits are required to identify the hosts. To do that I write the number of hosts required in binary. Here I will not be using byte-length binary numbers because the length of the number is important, and easier to see without leading zeroes.
Express requirement in binary;
40+1 hosts = 41 hosts
101001 hosts
Alright, so 101001 is a six-digit number. So I need six bits to define the hosts. Second rule: Bits are binary digits. So the number of binary digits used to express the host requirement is the number of bits we'll need to reserve for it. Third rule: what isn't the host is the network. Fourth rule: Network bits first, host bits second..
Now we can design our subnet mask:
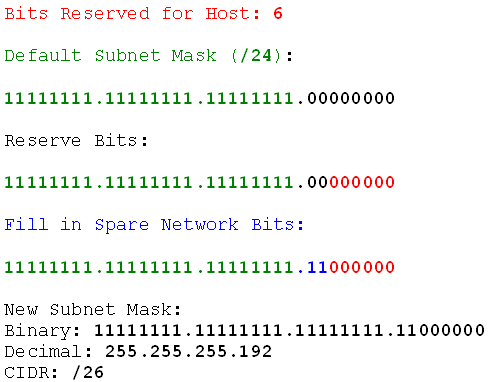
So what did I do there? I took the default subnet mask, reserved the host bits on the right, and filled in the unused and unreserved bits. That gave me the new subnet mask. Now I can find the network ranges. Fifth rule: network ranges start from the default network id and end with the default broadcast. So I'll find those.
Network: 192.168.0.0
Network ID (first address): 192.168.0.0
Broadcast (last address): 192.168.0.255
Now I know my start and end point, I need to know the increment. Sixth rule: the increment bit is the last bit in the subnet mask.
Binary Subnet Mask (/26): 11111111.11111111.11111111.11000000
Increment Byte: 4
Increment Bit: 64
So now I have all the information I need to get to work finding the network ranges. I know that I start from 192.168.0.0 and head towards 192.168.0.255 in increments of 0.0.0.64 (because the increment bit is in the 4th byte). I'm going to do that now:
Network IDs:
192.168.0.0
192.168.0.64
192.168.0.128
192.168.0.192
Now I have the start points I also have the end points, because they will be one less than the next network ID. So they're simple to fill in. What about the last end point, though? That's going to be one less than what the next network ID would be, if it were allowed. The next network ID would be 192.168.1.0, because 192.168.0.192+0.0.0.64 = 192.168.1.0 (the 192+64 make 256 which carries over as a 1 in the next byte, because 255 is the most we can have in any single byte). So what's one less than 192.168.1.0? Well just as we carried over adding, we also carry back when subtracting. You know what? I'm going to show you all that stuff I just said because it might make more sense then:

Hopefully that makes more sense now. Anyway, my ranges are done. Here they are:

All these networks have the same subnet mask: /26 (or 255.255.255.192).
I have 4 networks, and each network can support 62 hosts. We only needed 40, but we got 62. That happened because with the six bits I needed reserved for making 40 in binary I can actually make the number 63 if all six bits are 1. Take one away for the broadcast address and we're left with 62 possible addresses.
Subnet by Hosts - Example
Now we'll do a similar problem together. This time we'll be subnetting the 192.168.5.0 network into networks of 30 hosts each. Let's review our rules and process, then go for it.
Rules:
- always add 1 to the host requirement
- bits are binary digits
- what isn't the host is the network
- network bits first, host bits second
- the increment bit is the last bit in the subnet mask
Process:
- Analyse the problem (find requirement, default network, and default subnet mask)
- Adjust the requirement by rule 1
- Find number of digits needed to express the requirement in binary
- Reserve that many bits in the binary subnet mask
- Find the increment (column value of the last 1 in the subnet mask)
- Write down network IDs starting with default network id and ending when you go past the default broadcast address
- Fill in the broadcast addresses for the networks
- Done. You now have the networks and their subnet mask
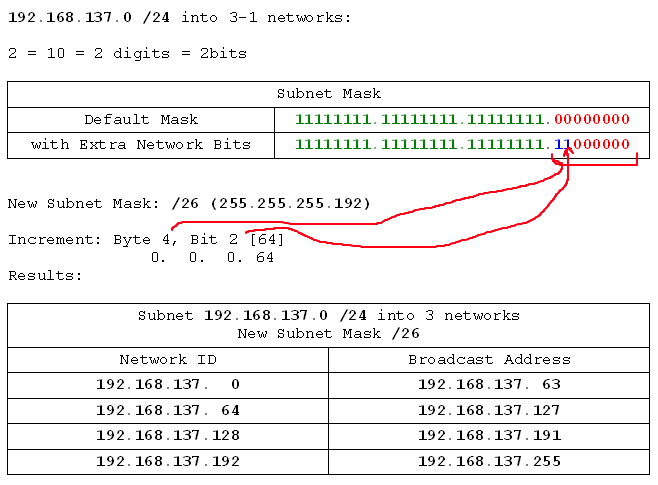
Right. Let's analyse the problem:
Network: 192.168.5.0 /24
Requirement: 30 hosts
Adjust for rule 1:
Network: 192.168.5.0 /24
Requirement: 30+1 hosts
Find reserved bits:
31 in binary = 11111
Number of digits = 5
Reserve bits in binary mask:
Mask: /24
11111111.11111111.11111111.000xxxxx
Fill in the unused and unreserved bits:
11111111.11111111.11111111.111xxxxx
New Mask:
11111111.11111111.11111111.11100000 = /27
Find the increment:
Binary Mask:
11111111.11111111.11111111.11100000
Increment Byte:
4
Increment Bit: 32
Fill in the network IDs, then broadcast addresses:
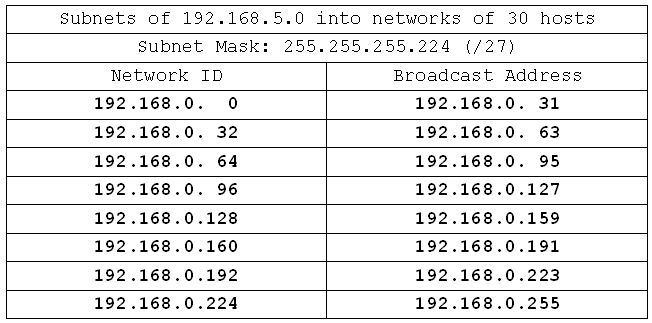
And we're done. Not all that much to it. Now we'll do some more complex exercises. Some of these will use non-class C networks, and some will result in having a great many networks. Feel free to shortcut and fill in only the first network IDs and broadcast addresses for the longer ones. I'll put detail in my examples of each new class in case you get into trouble with the adding and subtracting across bytes.
Exercise: Subnetting By Host Requirement:
Here are 10 subnetting examples for you. Don't worry if you're slow to begin with, but time yourself anyway. Once you get comfortable with the process of subnetting you should be able to subnet even class A networks in 2-3 minutes. Here are the questions, good luck.
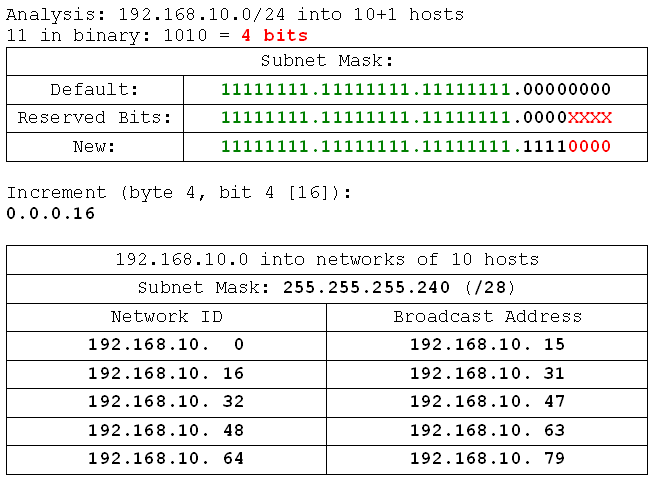
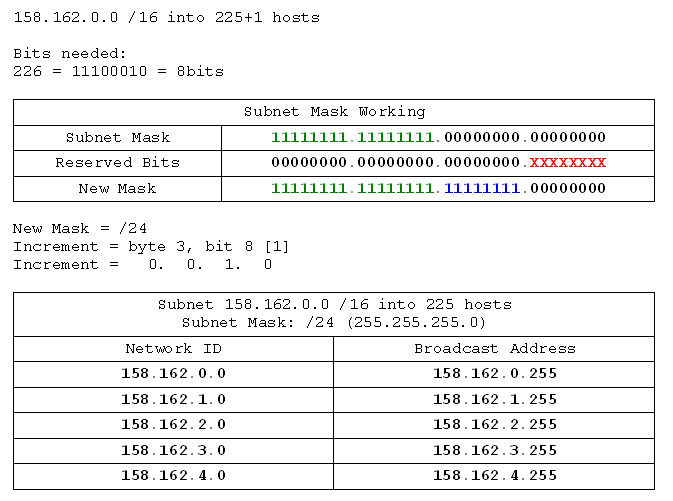
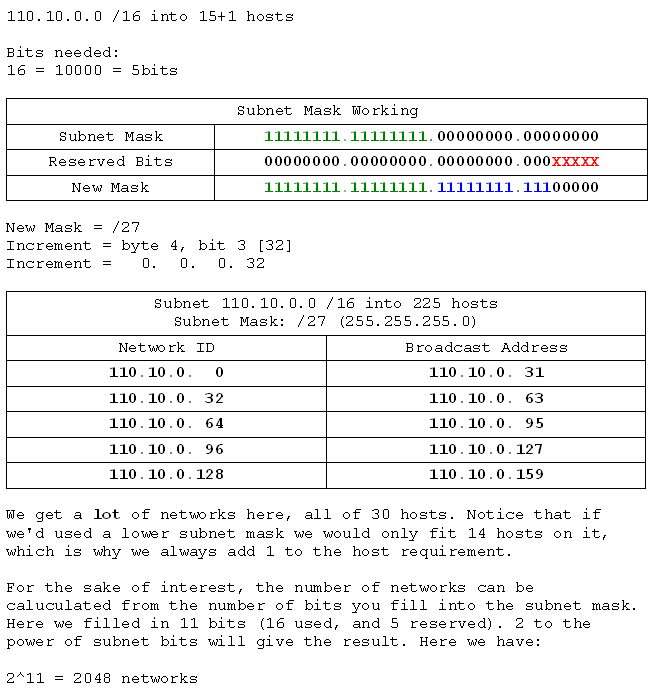
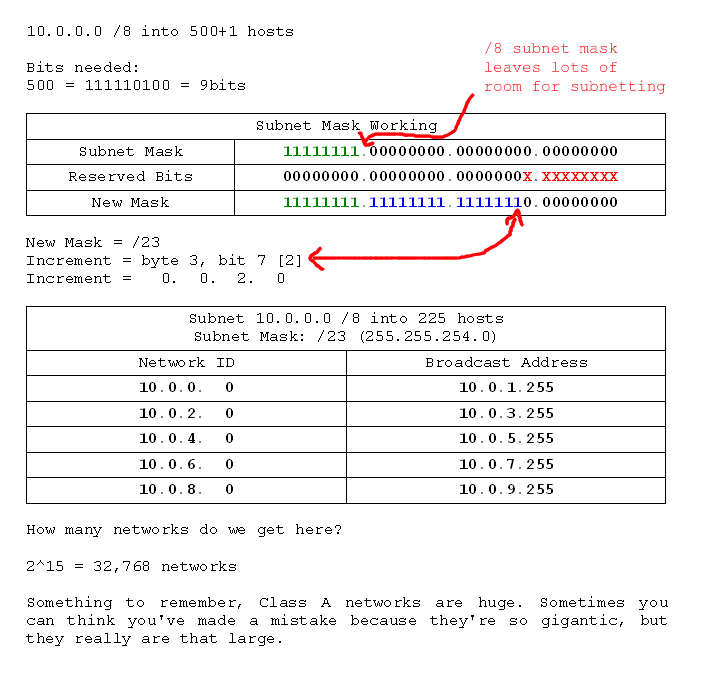
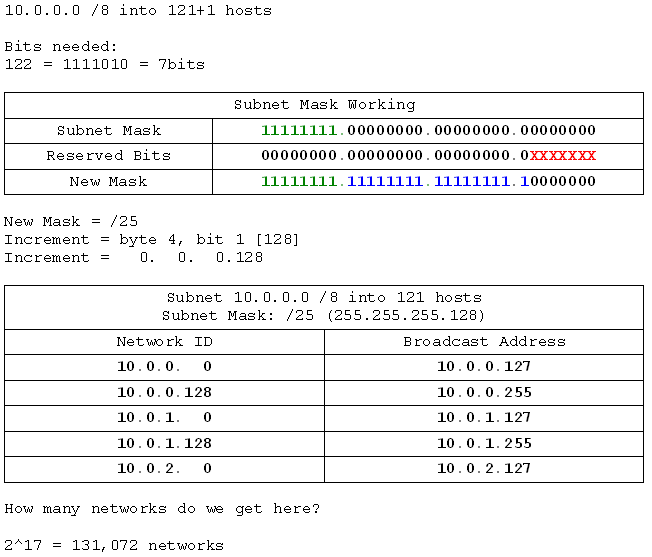
- 192.168.10.0 /24 into networks of 10 hosts
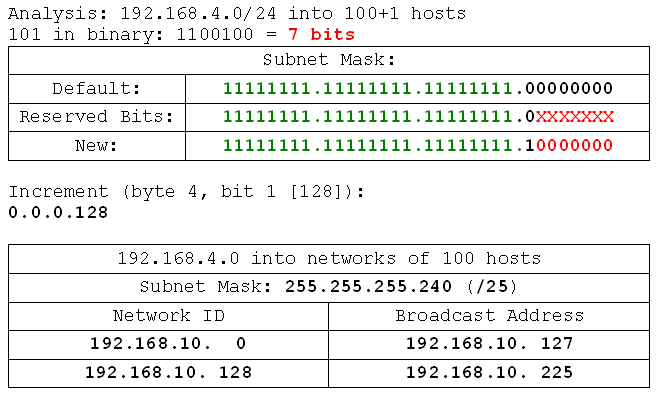
- 192.168.4.0 /24 into networks of 100 hosts
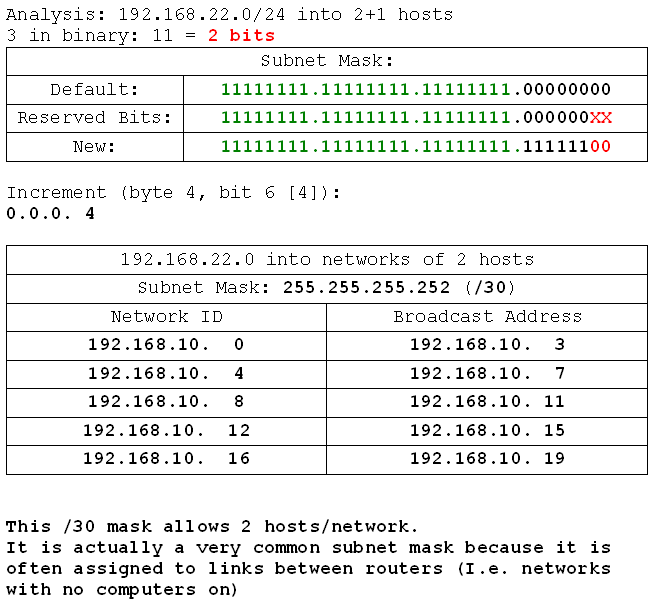
- 199.99.22.0 /24 into networks of 2 hosts
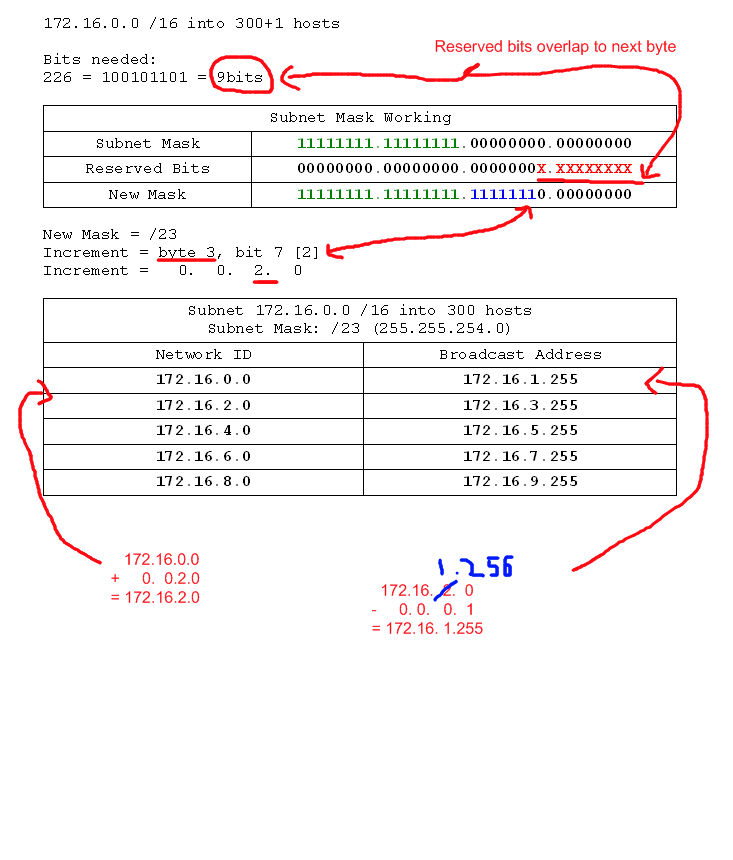
- 172.16.0.0 /16 into networks of 300 hosts
- 158.162.0.0 /16 into networks of 225 hosts
- 130.45.0.0 /16 into networks of 150 hosts
- 110.10.0.0 /16 into networks of 15 hosts
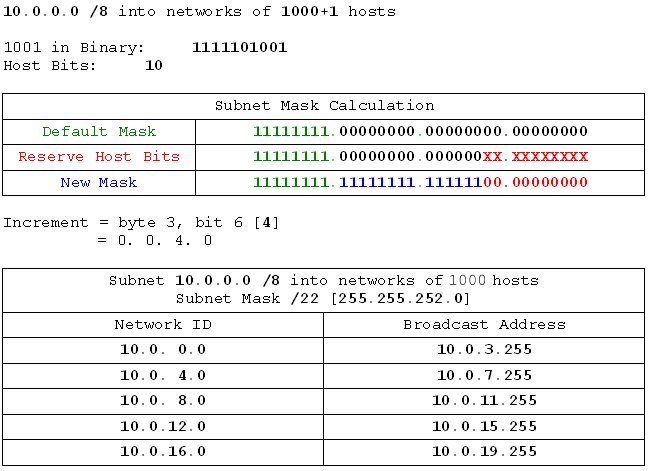
- 10.0.0.0 /8 into networks of 500 hosts
- 10.0.0.0 /8 into networks of 121 hosts
- 17.0.0.0 /8 into networks of 60 hosts
- 192.168.10.0 /24 into networks of 10 hosts
- 192.168.4.0 /24 into networks of 100 hosts
- 199.99.22.0 /24 into networks of 2 hosts
- 172.16.0.0 /16 into networks of 300 hosts
- 158.162.0.0 /16 into networks of 225 hosts
- 130.45.0.0 /16 into networks of 150 hosts
- 110.10.0.0 /16 into networks of 15 hosts
- 10.0.0.0 /8 into networks of 500 hosts
- 10.0.0.0 /8 into networks of 121 hosts
- 17.0.0.0 /8 into networks of 60 hosts
Summary
So by now we should be able to subnet based on a host requirement. If you're having trouble, try doing some more examples, and read through closely on the bits that seem to be going wrong. Once you get the hang of it it's not only easy, but fun! Or maybe that's just me. Next we'll learn how to subnet based on a required number of networks.
Part 5 - Subnetting by Networks
Introduction
We now know how to subnet when asked to make networks of a certain size. Here we will work out how to make a specific number of networks. The process is largely the same, so we'll just dive right in.
Subnetting by Network Requirement - Walkthrough
I've got the 198.220.40.0 network at my disposal. I decide that I need to split it into 6 different networks. Here's how I do it:
Analyse the problem:
Network: 198.220.40.0 /24
Requirement: 6 networks
First rule: Always subtract 1 from the network requirement. Why? Because like adding one to the host requirement to compensate for the broadcast address, we actually produce one more network than we subnet for because we number the networks from 1 and they start from 0. So if we were to subnet for exactly the right number of networks we might find we've made one too many.
Network: 198.220.40.0 /24
Requirement: 6-1 networks
The second, third, and fourth rules are the same as subnetting by hosts:
Bits are binary digits
What isn't the host is the network
Network bits first, host bits second
So I will have to find out how many bits I need to express the network requirement. As you've probably worked out before reading this sentence (which is longer than it needs to be to give you a little more time to work) the binary value for 5 is 101, which takes three bits to express. So we need three bits, but are they host bits or network bits? Network bits. So where do they go? Network bits first, host bits second. Alright, so I don't need to put my host bits in my subnet mask because they're already zero. We're already done:

Now what? Now I obey the third rule: what isn't the host is the network, or, equally true: what isn't the network is the host. So we have our subnet mask, because the host bits are left as 0.

Now I have my subnet mask the process is identical to the previous one. I find the increment, and calculate the networks starting at the base (198.220.40.0):
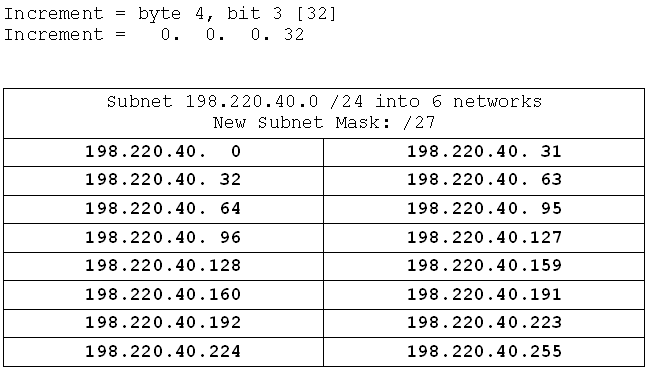
And that's it. So, what difference in the process is there? The only difference is in calculating the mask, and that difference is that when we're looking for hosts we reserve the bits (force them to be zero), and fill in the rest. When we're looking for networks we fill in the bits (force them to be 1), and leave the rest blank.
Alright, we should be ready for an exercise, but, as an added bonus, I'll give you the formula for working out how many hosts you will have when given a subnet mask. It's two to the power of the number of host bits (the 0s in the mask) minus two. So for my network above we'd get:
Host bits: 5
(2^5)-2 = 32-2 = 30 hosts/network. And what did we get? We got network ranges from 0-31, which gives us useable addresses 1-30. So 30 addresses/network. Excellent.
Exercises
Quite a short tutorial this time, because you already know almost all you need from the previous one. So let's do some exercises based on subnetting by networks. This time I've thrown a couple of subnet by hosts problems in the mix to keep you on your toes, so read the question carefully.
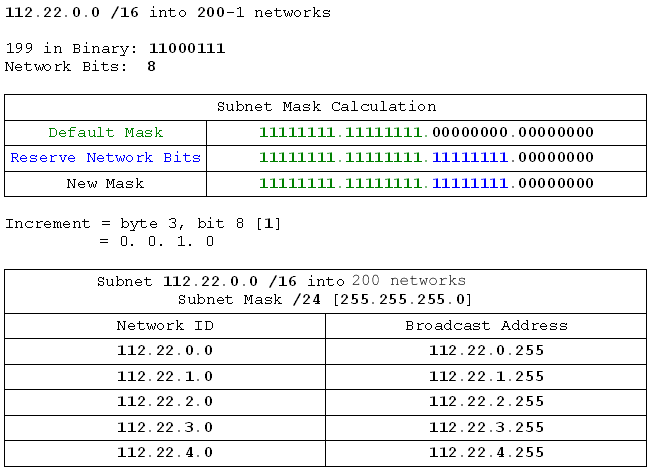
- 192.168.137.0 /24 into 3 networks
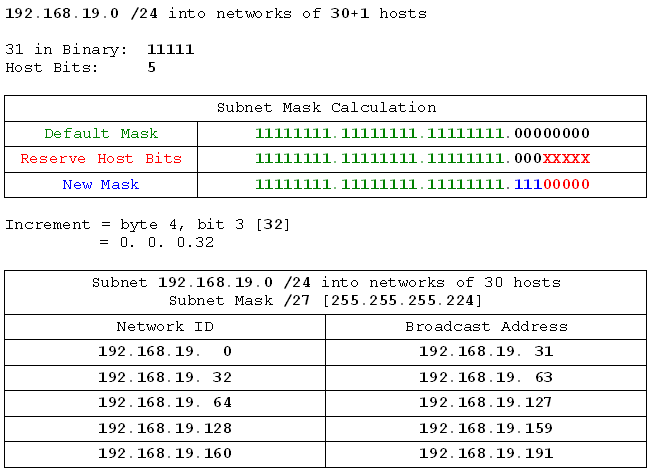
- 192.168.19.0 /24 into networks of 30 hosts
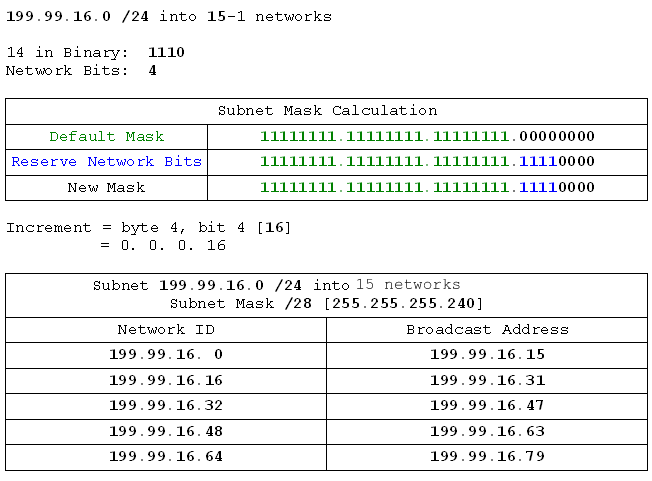
- 199.99.16.0 /24 into 15 networks
- 172.16.0.0 /16 into 100 networks
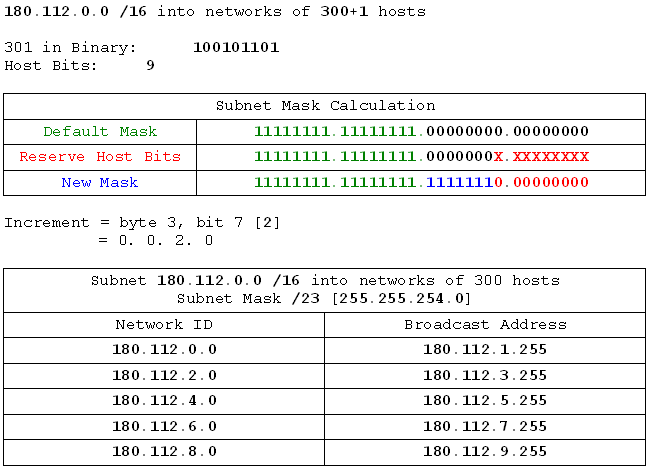
- 180.112.0.0 /16 into networks of 300 hosts
- 137.46.0.0 /16 into 6 networks
- 112.22.0.0 /16 into 200 networks
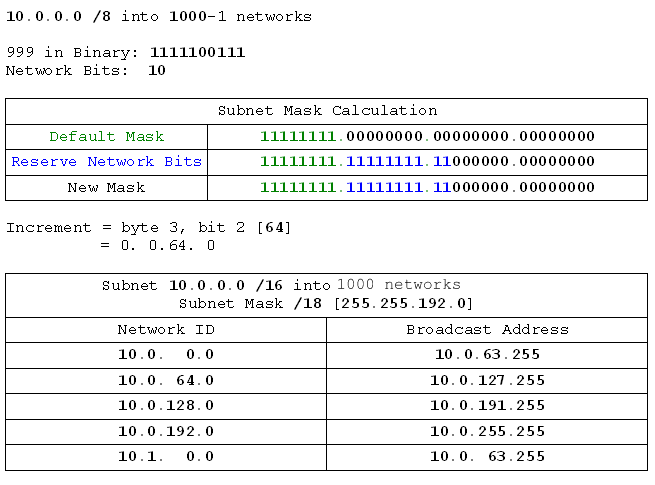
- 10.0.0.0 /8 into 1000 networks
- 10.0.0.0 /8 into networks of 400 hosts
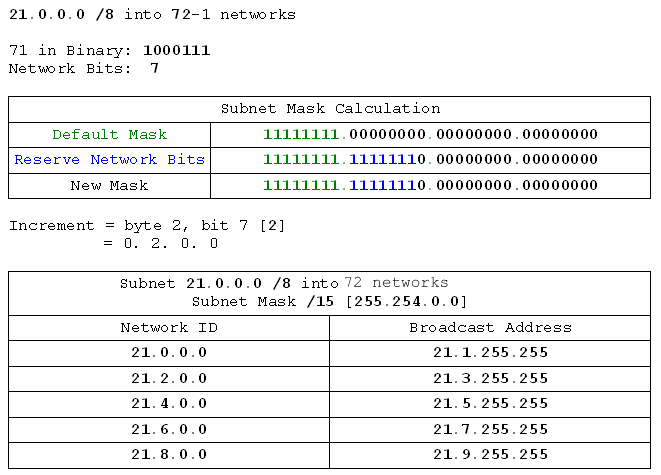
- 21.0.0.0 /8 into 72 networks
- 192.168.137.0 /24 into 3 networks
- 192.168.19.0 /24 into networks of 30 hosts
- 199.99.16.0 /24 into 15 networks
- 172.16.0.0 /16 into 100 networks
- 180.112.0.0 /16 into networks of 300 hosts
- 137.46.0.0 /16 into 6 networks
- 112.22.0.0 /16 into 200 networks
- 10.0.0.0 /8 into 1000 networks
- 10.0.0.0 /8 into networks of 400 hosts
- 21.0.0.0 /8 into 72 networks
Part 5 - Subnetting in the Real World (VLSM)
Introduction
Oooo-kay. We've covered subnetting by hosts and subnetting by networks. Now it's time to start using subnetting for some more realistic examples. For this we're going to need a handle on some new concepts such as network diagrams. We'll be using what is known as VLSM, or Variable Length Subnet Masks. We'll discuss network diagrams, then we'll look at VLSM and cover what it's used for and why it's so excellent. Then we'll roll up our sleeves and start addressing a network.
Glossary:
VLSM - Variable-Length Subnet Mask: a network addressed using a series of different subnet masks
Network Diagrams
A network diagram is essentially a map of a network. It can contain a lot of information, or merely a brief overview of the network. Because we're networking people, not customer support, network diagrams tend to omit hosts entirely. We sometimes put servers on the diagrams, but mostly it's used for routers and switches. We only need to know the basics of network diagrams here, so that's all we'll be covering. We're also only interested in routers, so we won't even be bothering with switches on our diagrams. Here's what we will be working with:
Routers
Host Networks
LAN links
WAN links
"The Internet"
And that's it. So let's look at a simple network diagram with all of those in place:
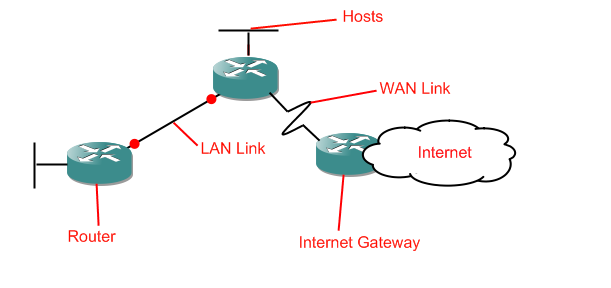
As you can see, the short fat cylinders are routers, the straight lines are LAN links, the jagged lines are WAN links, and the unfinished bits which run off into space are host networks. The big cloud is the internet. That's where we are right now. If you're cold that's because clouds generally are cold. Put on a jumper and drink more coffee. Anyway, that's network diagrams. Oh, and don't worry if later there are red dots on the LAN/WAN links, they're just there because I'll be using GNS3 to produce the diagrams (a great tool for learning router configuration, by the way).
Why do we need network diagrams? We'll be using them here because we'll be giving addresses to a bunch of different devices. Actually we won't be assigning addresses, instead we'll be handing out subnet masks and network IDs to various networks. The principle is the same, except this way we don't have to do the repetative boring bits.
We'll be starting off with a network diagram specifying the requirements which will look a little like this:
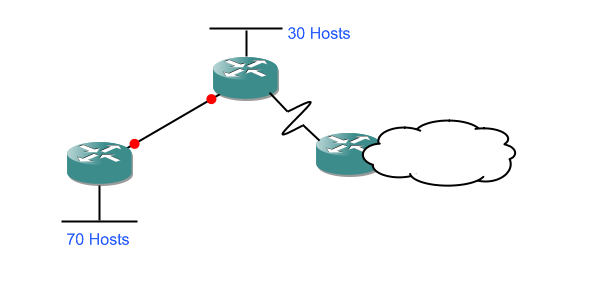
and ending up with a network diagram which has the network IDs and subnet masks filled in:
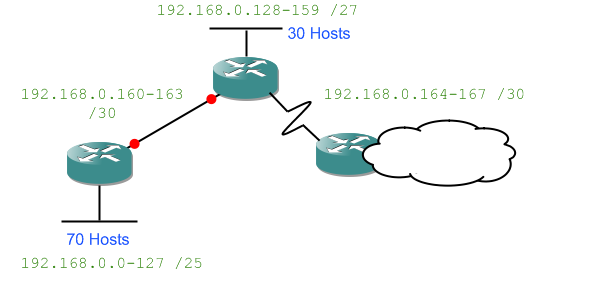
Something to note now because it'll be important later: the LAN links between routers are network. That means they need their own network ID and subnet mask.
VLSM
Why do we need VLSM? Remembering that LAN links between routers are networks gives us not only a clue but the answer itself. Imagine if we had a /24 network (giving us 254 possible addresses) and we wanted to split it up to address the diagram I gave above. We couldn't do it. The largest set of hosts is 70, so we'd need networks 192.168.0.0-127, 128-255, and now we've run out. Even though several of those networks only have two devices on them because they link a pair of routers. We've gone and wasted a massive number of addresses. With VLSM we address the entire network and still have almost 100 addresses left.
That is why we need VLSM. It allows us to conserve addresses by allocating a different size to each network depending on its requirement. So how does it work? Let's walk it through step by step, but first, we'll have an overview.
With VLSM we are giving each network only the number of addresses it actually needs. We do this by starting with the largest network and then proceeding on to the next largest, and so on. We analyse the task firstly by dividing it into a series of different subnetting problems, and then by approaching each one in turn. So let's get an example going...
Walkthrough
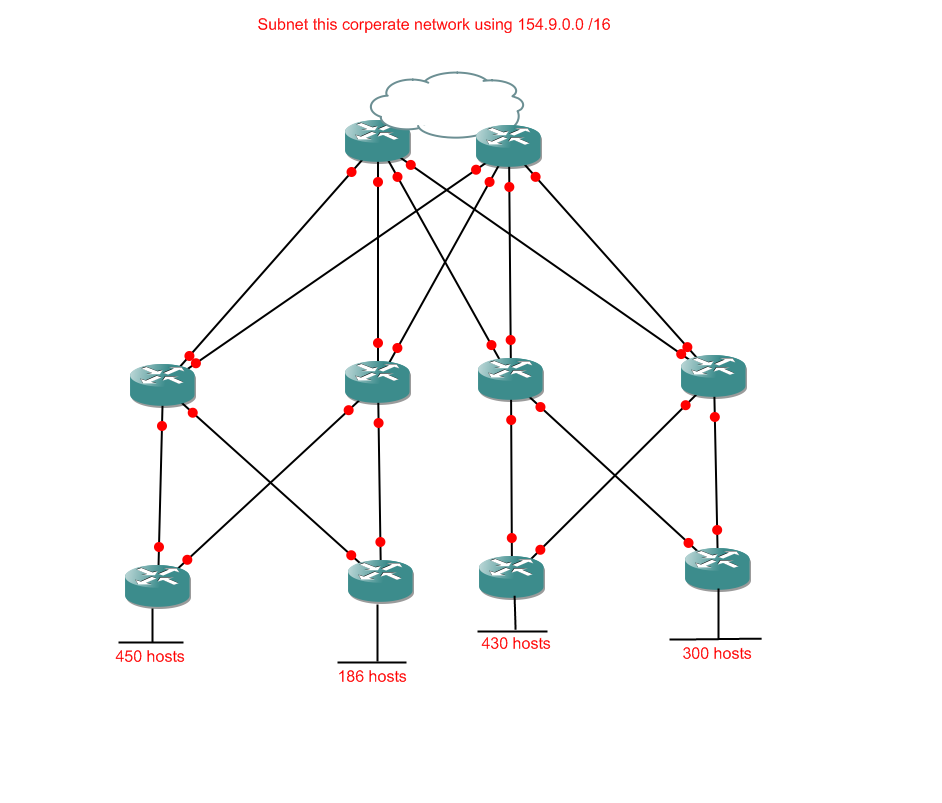
Here is a network diagram:
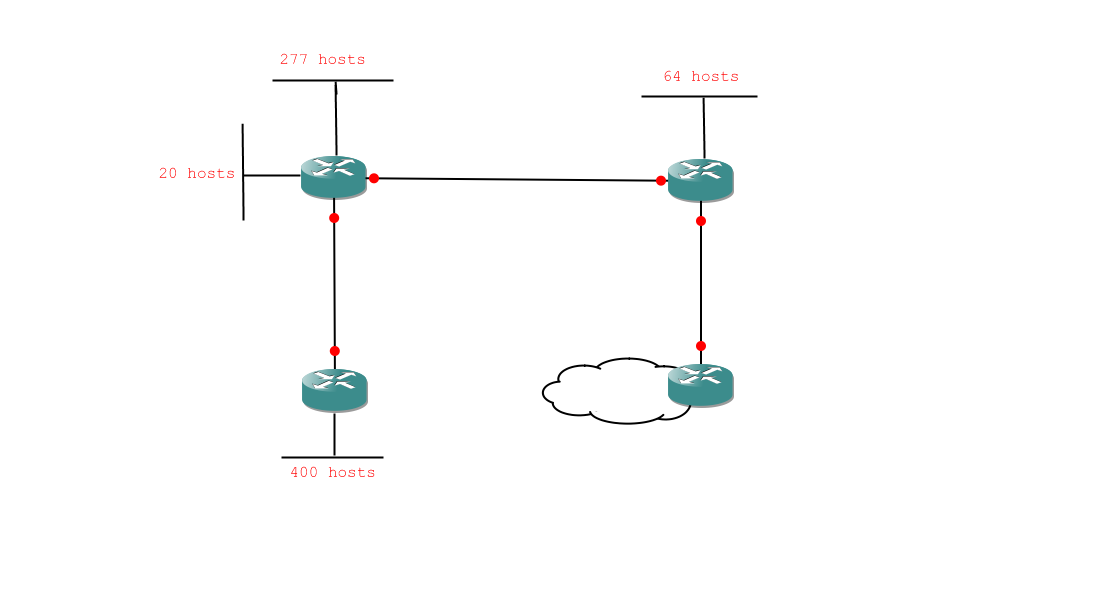
And here is the diagram with my analysis notes scribbled all over it:
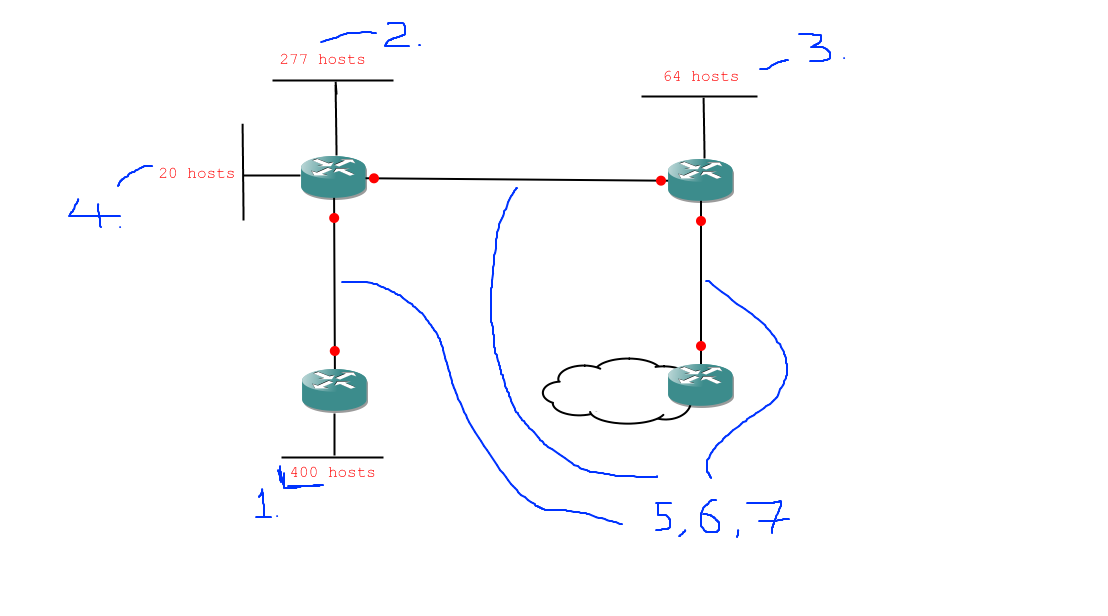
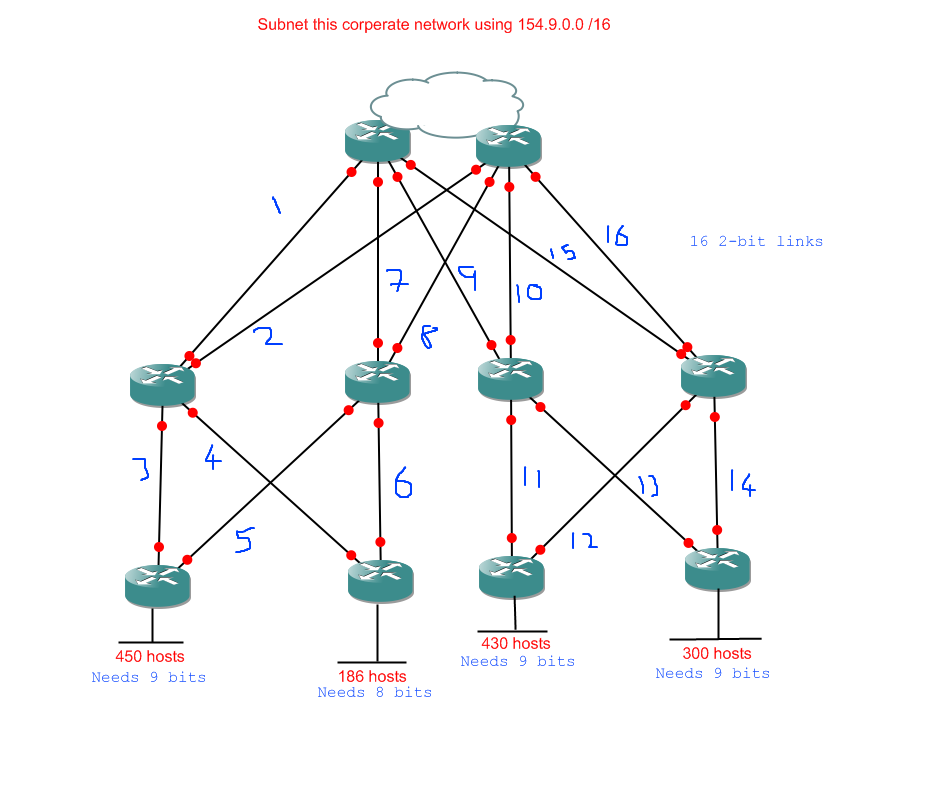
So, here are the subnetting tasks we need to deal with, in order:
- 1 network of 400 hosts
- 1 network of 277 hosts
- 1 network of 64 hosts
- 1 network of 20 hosts
- 3 networks of 2 hosts
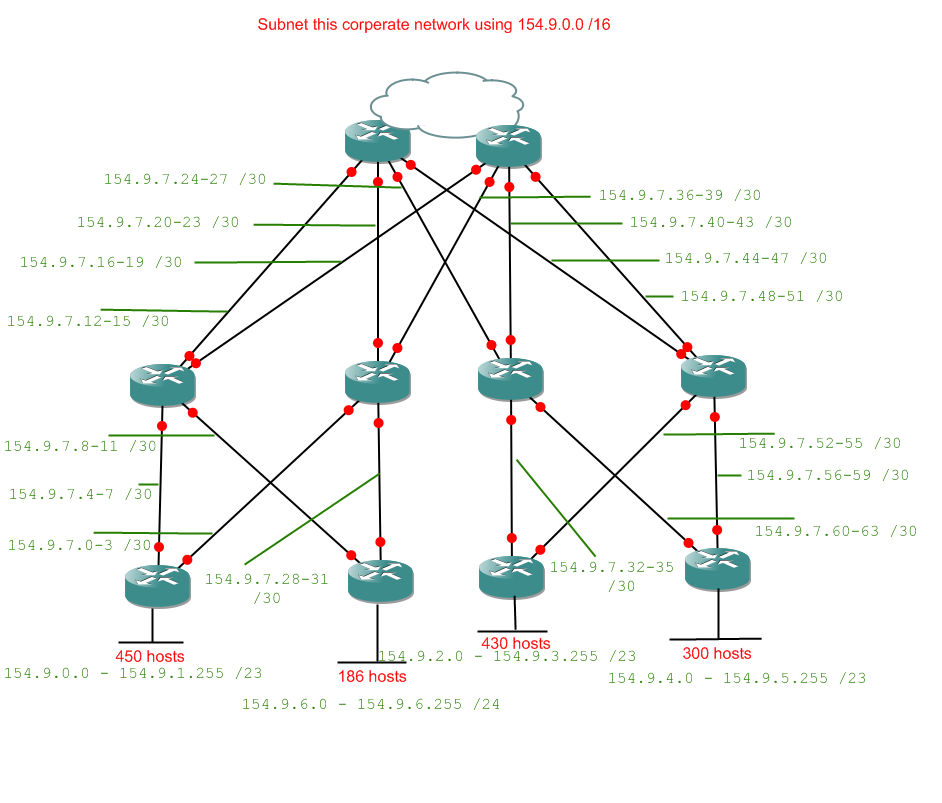
Obviously we can't do this with a /24 network (which would only give us 254 useable addresses) so we'll be using a /16 network: 172.16.0.0 /16. So, our first problem is 172.16.0.0 /16 into networks of 400 hosts. Quickly through that:
400+1 takes 9 binary digits to express.
9 bits reserved for hosts gives:
11111111.11111111.11111110.00000000
Byte 3, bit 6 is our increment [2]
Increment is 0.0.2.0
Network range: 172.16.0.0 - 172.16.1.255
Subnet mask: 255.255.252.0 (/22)
Network: 172.16.0.0 - 172.16.1.255 /22
Now we fill that in and look at the second problem. We can't start the next subnet from 172.16.0.0 because 0.0 - 1.255 are already taken. So we'll have to start it from 172.16.2.0 (the first available address):
172.16.2.0 /22 into networks of 277 hosts:
277+1 takes 9 binary digits to express.
Ah, nice. The mask will be the same, as will the increment, so this step is easy.
Network: 172.16.2.0 - 172.16.3.255 /22
What happened there? Well we discovered that as far as binary is concerned it takes the same number of bits to express 277 as it does 400.
401: 110010001
278: 100010110
Both 9 digits
So we didn't actually need to do the work because we'd already done it. Once we have the subnet mask and increment it's simply a case of sticking the network into our list of networks starting from the first available address, which we did.
Next task (this one won't be quite so easy):
172.16.4.0 /22 into networks of 64 hosts:
64+1 takes 7 binary digits to express.
8 bits reserved for hosts gives:
11111111.11111111.11111111.10000000
Byte 4, bit 1 is our increment [128]
Increment is 0.0.0.128
Network range: 172.16.4.0 - 172.16.4.127
Subnet mask: 255.255.255.128 (/24)
Network: 172.168.4.0-127 /25
Notice I contracted 172.16.4.0 - 172.16.4.127 into 172.16.4.0-127. That is pretty standard practice. Sometimes you'll see multiple bytes contracted (we could have written 172.16.0.0 - 172.16.1.255 as 172.16.0.0-1.255), but it gets a little confusing, so we'll stick with single-byte contraction.
Next we have the last of our hosts to deal with, then all we have left are the links between routers.
172.16.4.128 into networks of 20 hosts
20+1 takes 4 bytes to express
4 bits reserved for hosts gives:
11111111.11111111.11111111.11110000
Byte 4, bit 4 is our increment [16]
Increment is 0.0.0.16
Network range: 172.16.4.128 - 172.16.4.143
subnet mask: 255.255.255.240 (/28)
Network: 172.16.4.128-143 /28
And now we only have the final three router links to complete. You'll get to know those off by heart, but let's just do the thing in full this time through:
172.16.4.144 /28 into networks of 2 hosts:
2+1 takes 2 bits to express
2 bits reserved for hosts gives:
11111111.11111111.11111111.11111100
Byte 4, bit 6 is our increment [4]
Increment is 0.0.0.4
Network range: 172.16.4.144 - 172.16.4.147
Subnet mask: 255.255.255.252
Networks:
172.16.4.144-147 /30
172.16.4.148-151 /30
172.16.4.152-155 /30
And we're done. A lot of subnetting there, but we've managed to address our entire network with only a tiny fraction of our allotted 172.16.0.0 /16 range. Let's see the diagram filled in:
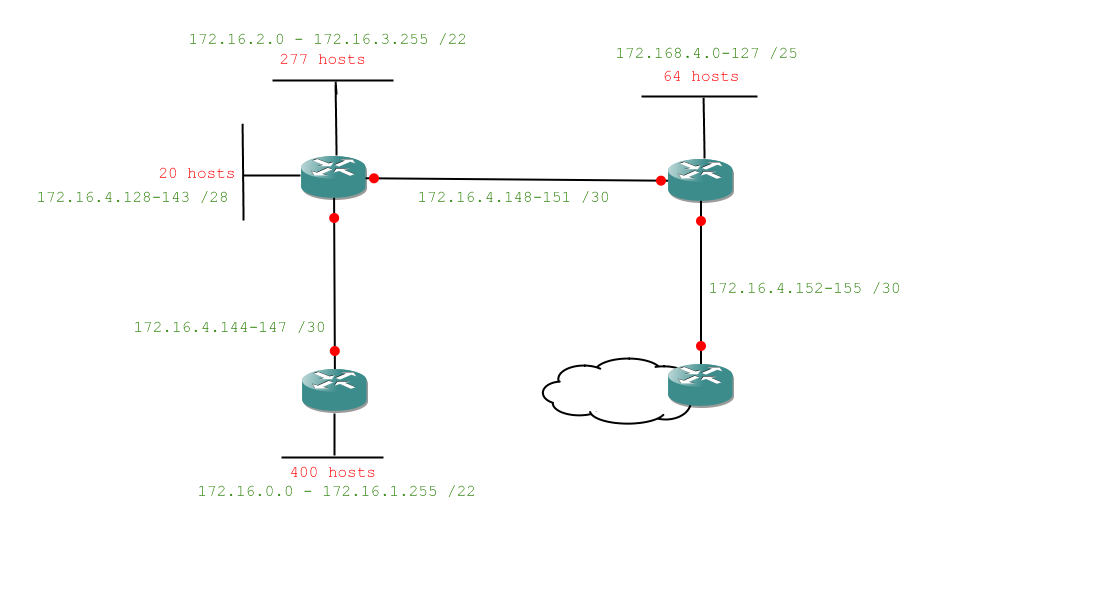
Wow. Quite a lot there, but is it making sense? Let's have a go at an exercise and see if we both get the same answer.
Step-by-step Exercise
So, here's the question:
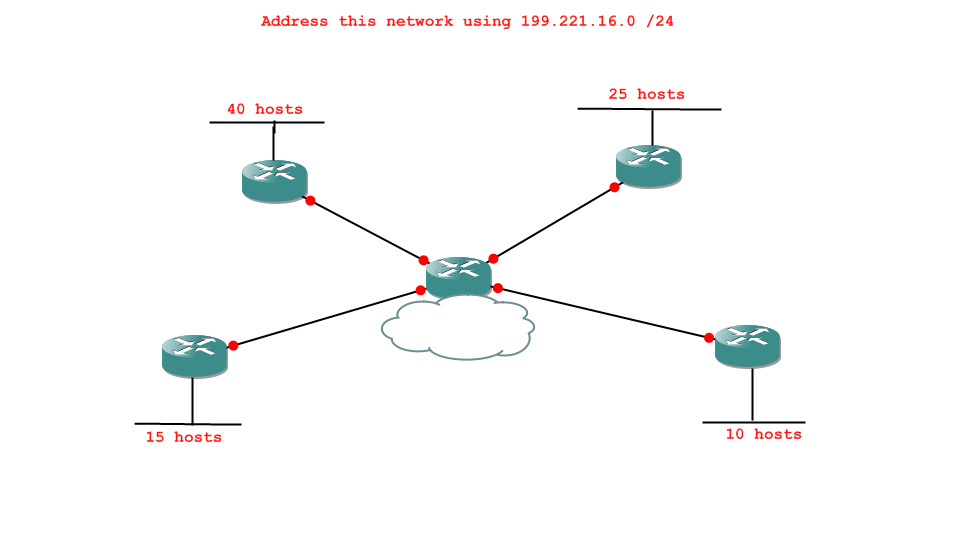
First, the initial analysis. What are the tasks we will have to complete, in order?
Check your answer -
- 1 network of 40 hosts
- 1 network of 25 hosts
- 1 network of 15 hosts
- 1 network of 10 hosts
- 4 networks of 2 hosts
Okay, so what's the first task? Your answer should look like "subnet [some network] into networks of [some number of hosts]".
Check your answer -
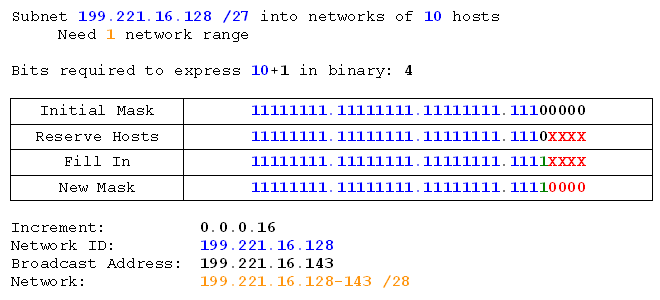
Subnet 199.221.16.0 /24 into networks of 40 hosts.
So we do that. Remember we only need 1 network, so we only need the first network range (network id - broadcast id /mask).
Check your answer -
Good. Okay, so what's our next task?
Check your answer -
Subnet 199.221.16.64 /26 into networks of 25 hosts.
Why? Because we've already assigned 199.221.16.0-63 in the previous task. We can inherit the subnet mask to remind ourselves where we are (hence /26 rather than /24), but it doesn't matter too much if we don't (provided we have the tasks in the right order). Incidentally, the one really useful thing keeping the last mask does is let us know if we've got too many hosts on a network (i.e. not enough addreses).
Anyway, yes. We've already assigned 199.221.16.0-63, so we'll start with 199.221.16.64 /26 and subnet that.
So we do that task...
Check your answer -
Good. So the next task is...?
Check your answer -
Subnet 199.221.16.96 /27 into networks of 15 hosts.
Again we start from the first useable address (the previous ones are already assigned), and we inherit the subnet mask.
We do that task.
Check your answer -
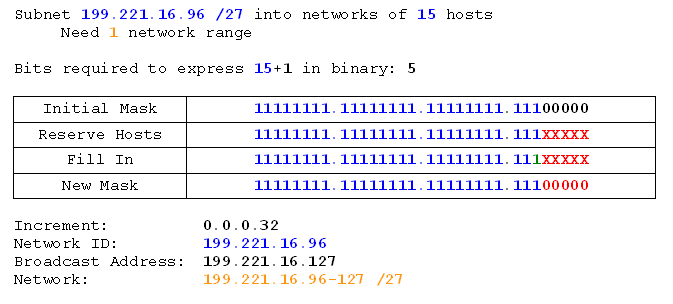
Notice that the mask didn't actually change. We could have noticed that it wasn't going to earlier. Maybe you did. On the next exercise we'll look at a neat short-cut to work that out ahead of time which will help us subnet faster.
Now we work out the last of our tasks before we get to the router links. Ready?
Check your answer -
Subnet 199.221.16.128 /27 into networks of 10 hosts.
We do that.
Check your answer -
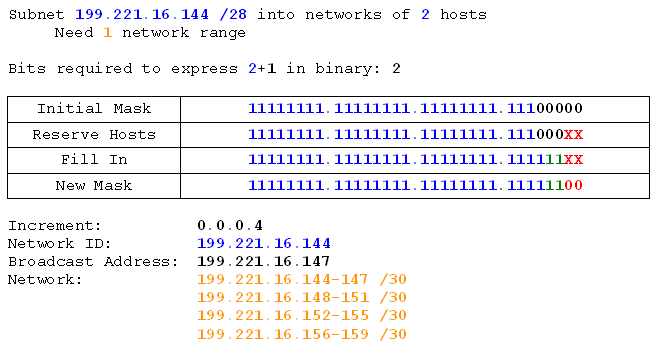
And finally we work out the task for our router links. Done?
Check your answer -
Subnet 199.221.16.144 /28 into networks of 2 hosts.
We do that and we get...
Check your answer -
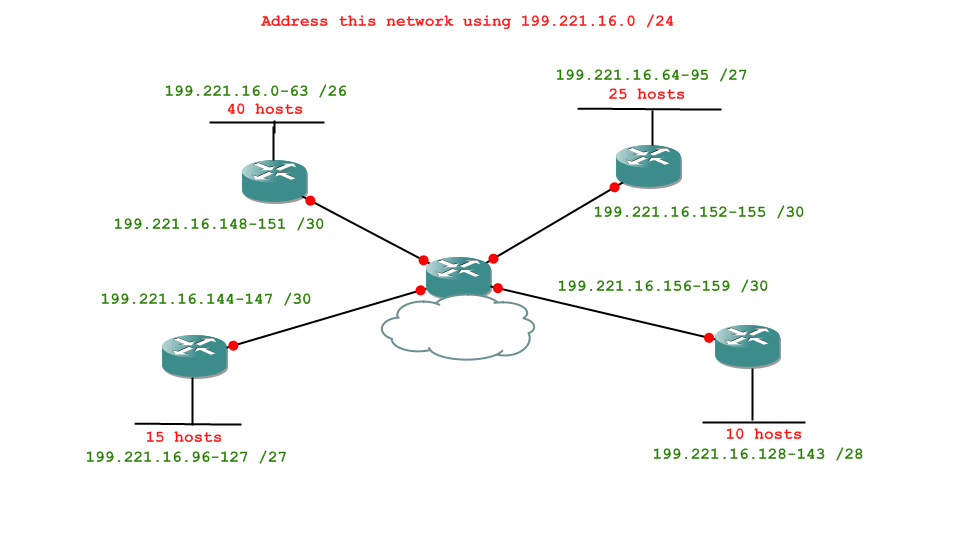
And finally we can fill in our network diagram. I actually do this after completing each task, or I would if I were doing it on paper, anyway. That way you don't have to search among your scribbles for the network ranges.
The final network diagram, then, would look like this:
Excellent.
Now we'll do one more exercise discussing a short-cut and some good general practice, and then I'll give you one big final exercise to do on your own.
Exercise with short-cuts and best-practice
Firstly, it's always good practice to use predicted host numbers rather than the number of hosts actually connected to a given network. The reason is simply that if a network needs to expand over its limit you'll have to go back to the subnet drawing board, and that's not a good thing to be doing every couple of months. It's not so much the subnetting as the continual reconfiguring of every device on your network.
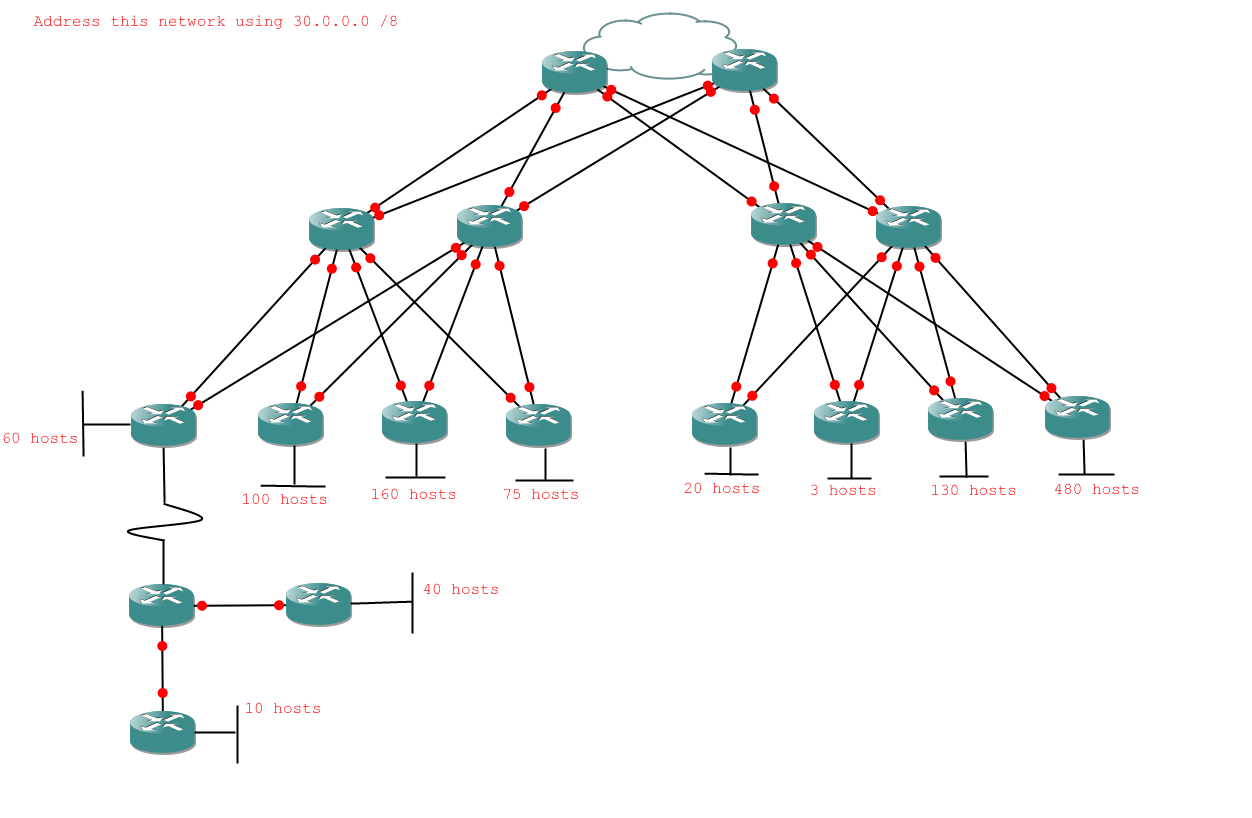
The other 'best practice' bit doesn't actually refer to subnetting at all, more to the way in which networks are built. Most medium and large (or at least large) networks have redundancy. That means that they are set up to survive network links going down, and even router crashes will only take out a small portion of the network. Network diagrams with redundancy tend to look complicated, but the approach to subnetting is exactly the same, only with more links between routers. Let's have a look at one:
Okay. I should probably mention that this is the point most people wish they hadn't started. I'd like to say it looks more complicated than it is, but it doesn't. It actually looks less complicated than it is, but only if you actually have to set the thing up. Then you have to deal with all sorts of things like Spanning Tree Protocol. The good news is that for our purposes it definitely is more complicated than it looks. Time to crack our knuckles and get subnetting.
First we analyse the problem. This time I'll show you the short-cut where instead of writing the number of hosts required for each network I write the number of bits required to express the host requirement instead. That will show me quickly which networks will end up with the same subnet mask. I also know by now that router links have only 2 required bits.
Alright, so here's what I've got for my tasks:
- 3 networks with 9 host bits
- 1 network with 8 host bits
- 16 networks with 2 host bits
You should be able to do those tasks alone by now, so when you're done check your answer below.
If you got the same as me, well done. If not, try to work out where you went wrong. Really something like this is no harder than the earlier examples, there are just more opportunities to make careless mistakes. There are useful checkpoints along the road, because of the way binary works. You will become accustomed to the sorts of numbers which make sense and which appear often. For now just be aware that the last byte of network IDs will always be even, and the last byte of broadcast addresses will always be odd. If they're not, check your answer because it's wrong.
All in all, well done. Time to leave you with a monster to bring home triumphantly.
VLSM - Final Exercise
Alright, here's the question. No help on this one, be careful and you should be alright.
Question:
Answer:
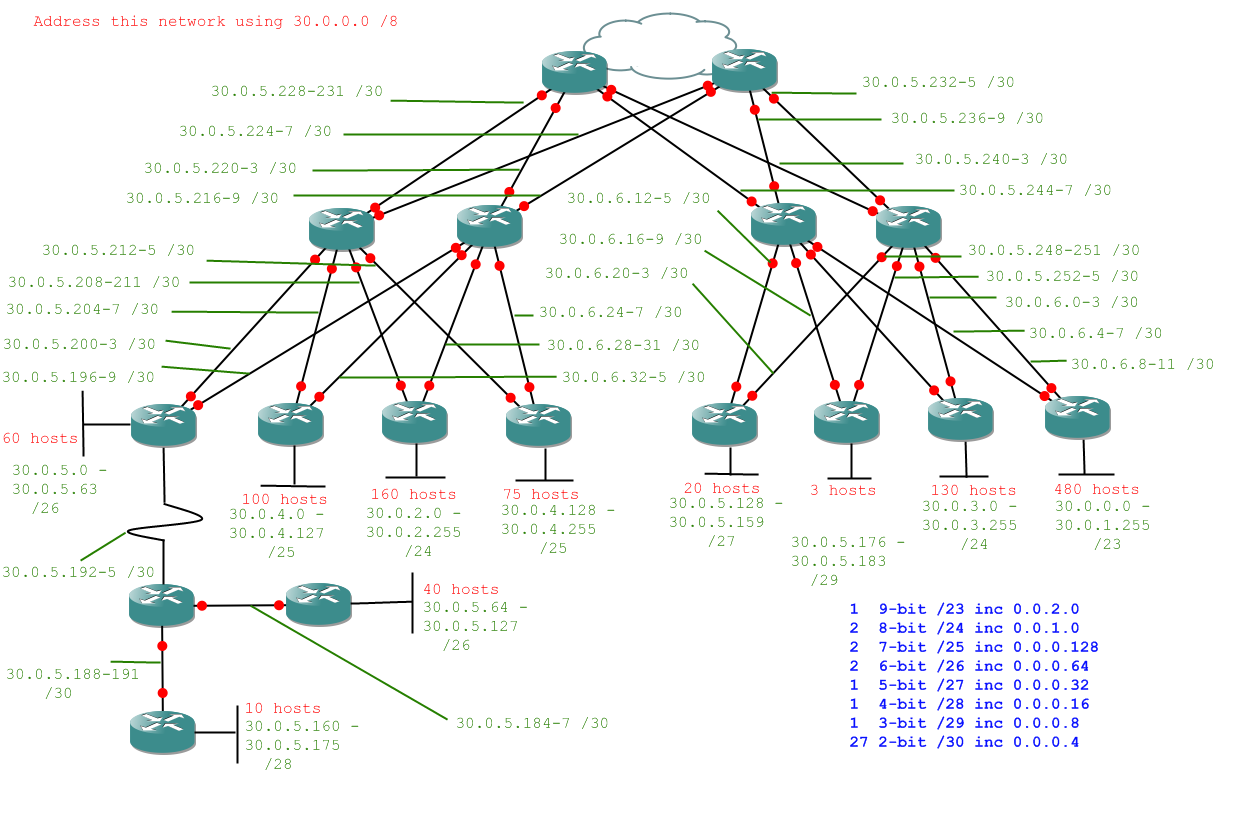
So long as you didn't fall into the trap of forgetting ot carry 256 over to a 1 in the previous byte you should have managed to do that without too much difficulty. If you did, well done.
Summary
We took a look at network diagrams, what VLSM is and what's so great about it, and how to do it. We tackled realistic networks with redundancy. We did all that and those of you who are still reading stuck with it the whole way. Well done.
The next and final part of this course will be simple in comparison - reverse engineering subnets, or finding the network range from the IP address and subnet mask
Part 7 - Debugging / Reverse-Engineering
Introduction
The end is in sight now. This is the last thing we have to learn - debugging subnet-based networking issues by reverse-engineering the IP address and subnet mask to determine the network ID and broadcast address. As we may remember from the very beginning of the course, a device can only communicate with something on a network it belongs to. If it wants to get off a network it needs a default gateway on its network to route its messages off that network.
This last section shouldn't take us too long. We'll look at a couple of problems we might have with incorrect IP address/Subnet Mask/Default Gateway combinations, how we'd diagnose them, and solving them should be easy by now. We already know how to solve them because unlike the ham-fisted git who set up a device with bad IP values we know how to subnet correctly.
Glossary:
Reverse-Engineering - Obtaining component parts and/or processes from an complete object.
Problems
There are only really two problems we can run into which we can detect by reverse engineering an IP address and subnet mask. The first is an invalid IP address. This occurs when a device is given an IP address which is not in the allowable range, i.e. the device has an IP address which is either the network ID or the broadcast address.
The second problem is when a device has a default gateway which is not on its network. When this happens the device will be unable to contact its default gateway because a default gateway provides a way off its network, which it can't access because it would need a default gateway to get to its default gateway. That may sound convoluted, but it's the computer equivalent of catch-22.
Reverse-Engineering Technique
What we need when trying to diagnose the problems discussed above are the network ID and broadcast address of our device's network. We can get these from combining what we know of the subnet mask and the IP address. As we know from subnetting, the subnet mask can tell us the increment between networks. The IP address can tell us what network class we're using (the starting point from which we increment) and which of those subnets we're on.
Let's look at an example:
IP Address: 192.168.0.32
Subnet Mask: 255.255.255.248
Default Gateway: 192.168.0.30
That's our IP info. Let's get to work. First we'll need to identify the network class (and therefore starting point) and increment. The network class we should know by heart from earlier. 192.168.* are private class C addresses, so this one will be the private class C network of 192.168.0 and will start from 192.168.0.0.
The increment we can retrieve by converting the subnet mask to binary:
255 - 11111111
255 - 11111111
255 - 11111111
248 - 11111000
So we know the binary subnet mask is 11111111.11111111.11111111.11111000, and therefore we know the increment is the value of the last 1 in the subnet mask: byte 4, bit 5 [16]. So now we start the process of working from our start point by increments until we reach our network.
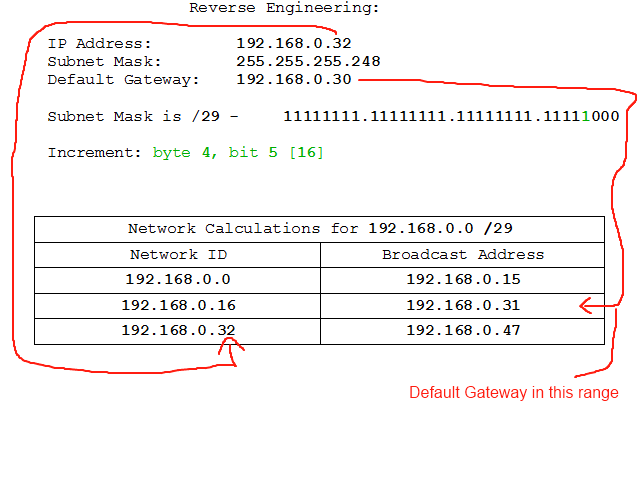
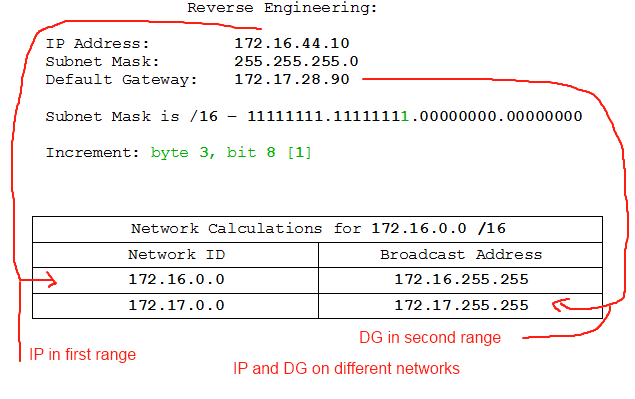
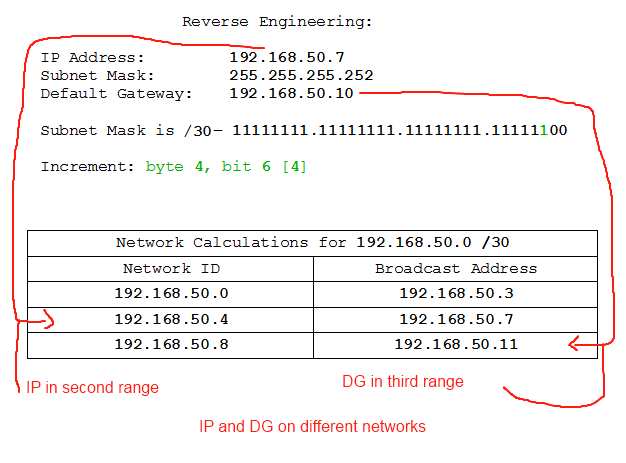
There. It turns out that the IP address assigned to the device is the network ID for that subnet. 192.168.0.32-47 is the network range, and the first address is the network ID which is what we have assigned to the device. The viable addresses in that range, however, are 192.168.0.33-46. If we look closely we'll also see that the Default Gateway, 192.158.0.30, is on a different network. So that's wrong, too. Pity the muppet who set this up.
That, believe it or not, is all there is to reverse-engineering subnets, really. When dealing with VLSM subnets we usually have a lot more legwork to do because of the way VLSM works (larger networks into smaller ones), but the principle is the same. Let's look at another example on a class A network and then dive right into the exercises. Notice we're presented with the same information, and we can't actually tell whether VLSM is active on the network. All we know is what we're given: IP Address, Subnet Mask, and Default Gateway. That's all we need, though, so we can't complain.
So, here's what we've got:
IP Address: 18.64.88.176
Subnet Mask: 255.0.0.0
Default Gateway: 18.255.255.255
If we're properly familiar with binary we should be able to tell immediately what the problem is here, but let's go through the steps anyway:
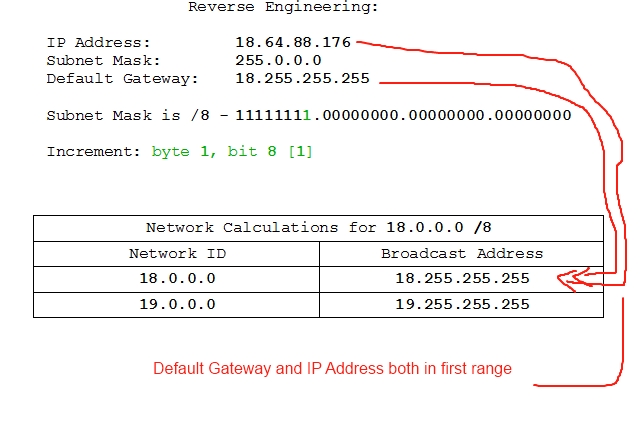
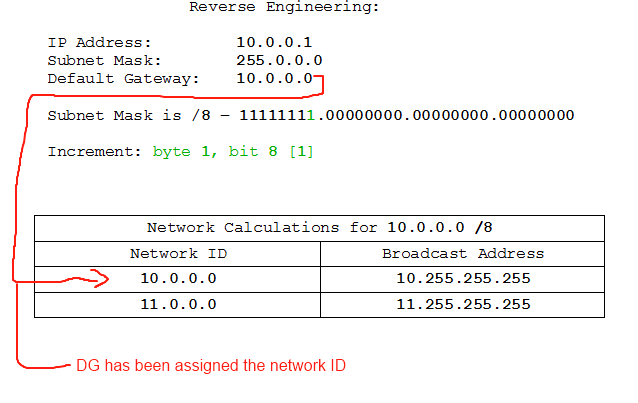
At this point you're forgiven for thinking "WTF? We have the default gateway and the IP address on the same network, and the IP address isn't the network ID or the broadcast address, so WTF is the problem?". The problem here, as you may have spotted by now, is that the default gateway has been assigned the broadcast address. The broadcast address and network ID are reserved addresses meaning that no device may occupy them. We've been alerted to the problem on a machine which is set up correctly, at least from its own point of view, but the actual problem is in the address assigned to the Default Gateway. Sometimes problems come at you back-to-front, but a logical reconstruction of the processes the machines are going through will get you to the solution in the end.
Exercises
Hopefully that's sunk in enough to get you through the following examples. We've only got a few this time because there really aren't that many variations on what can go wrong here and we don't want to get repetative. All I need by way of an answer is an identification of the problem, but you can give yourself extra credit if you show your working. Questions are in the form of IP: x.x.x.x /yy, DG: z.z.z.z where x.x.x.x is the IP, /yy the subnet mask, and z.z.z.z the default gateway.
- IP: 172.16.44.10 /18, DG: 172.16.28.90
- IP: 10.0.0.1 /8, DG: 10.0.0.0
- IP: 192.168.50.7 /30, DG: 192.168.50.10
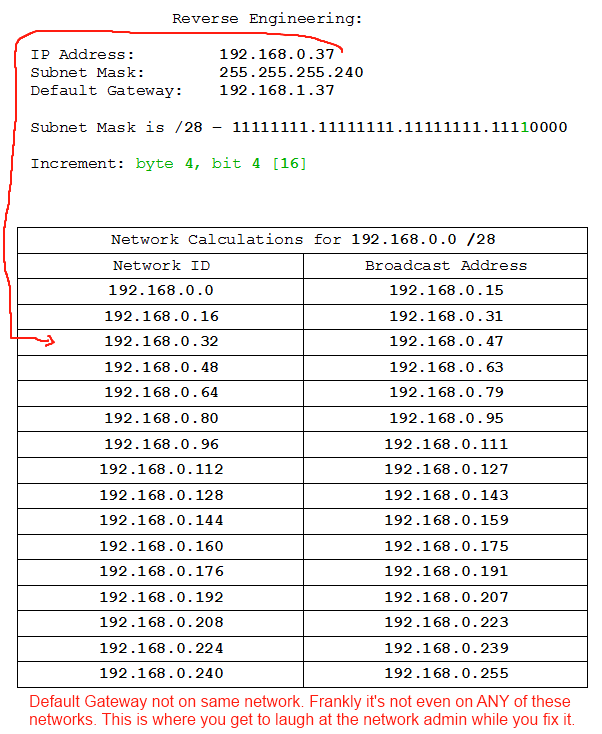
- IP: 192.168.0.37 /28, DG: 192.168.1.37
And the answers:
- IP: 172.16.44.10 /18, DG: 172.16.28.90
- IP: 10.0.0.1 /8, DG: 10.0.0.0
- IP: 192.168.50.7 /30, DG: 192.168.50.10
- IP: 192.168.0.37 /28, DG: 192.168.1.37
Summary
That concludes my course. Hopefully you've learned something useful, and some of you may have learned something you will use almost daily for the rest of your working lives. I'm sure I've kept you long enough, so I'll let you get on with the other things I'm sure you have to do. Just remember - Subnetting is FUN! Seriously, I love it.
Thank you for reading.
Obfuscater